Party Parrot waves and Collection rotations

Updates:

3/14/21:

Soroush messaged that using RangeReplaceableCollection’s + overload unfortunately incurs a copy. I’ve added a footnote¹ with his workaround that coincidentally uses John’s hint at the end about leaning on the square’s symmetry across the diagonal.

Joe Spadafora sent an emoji masterpiece in our team’s Slack the other day that doubled as a code golf.

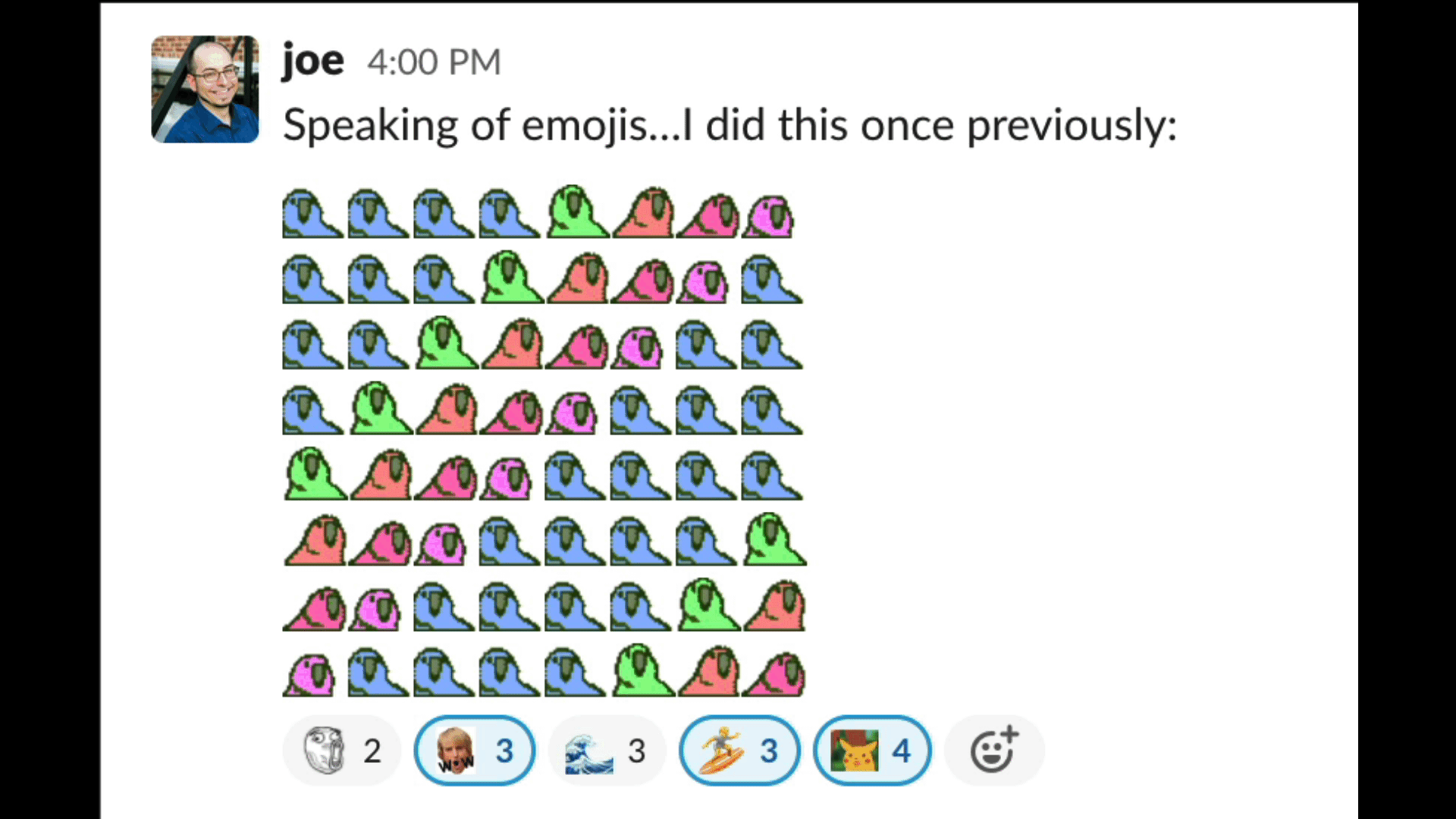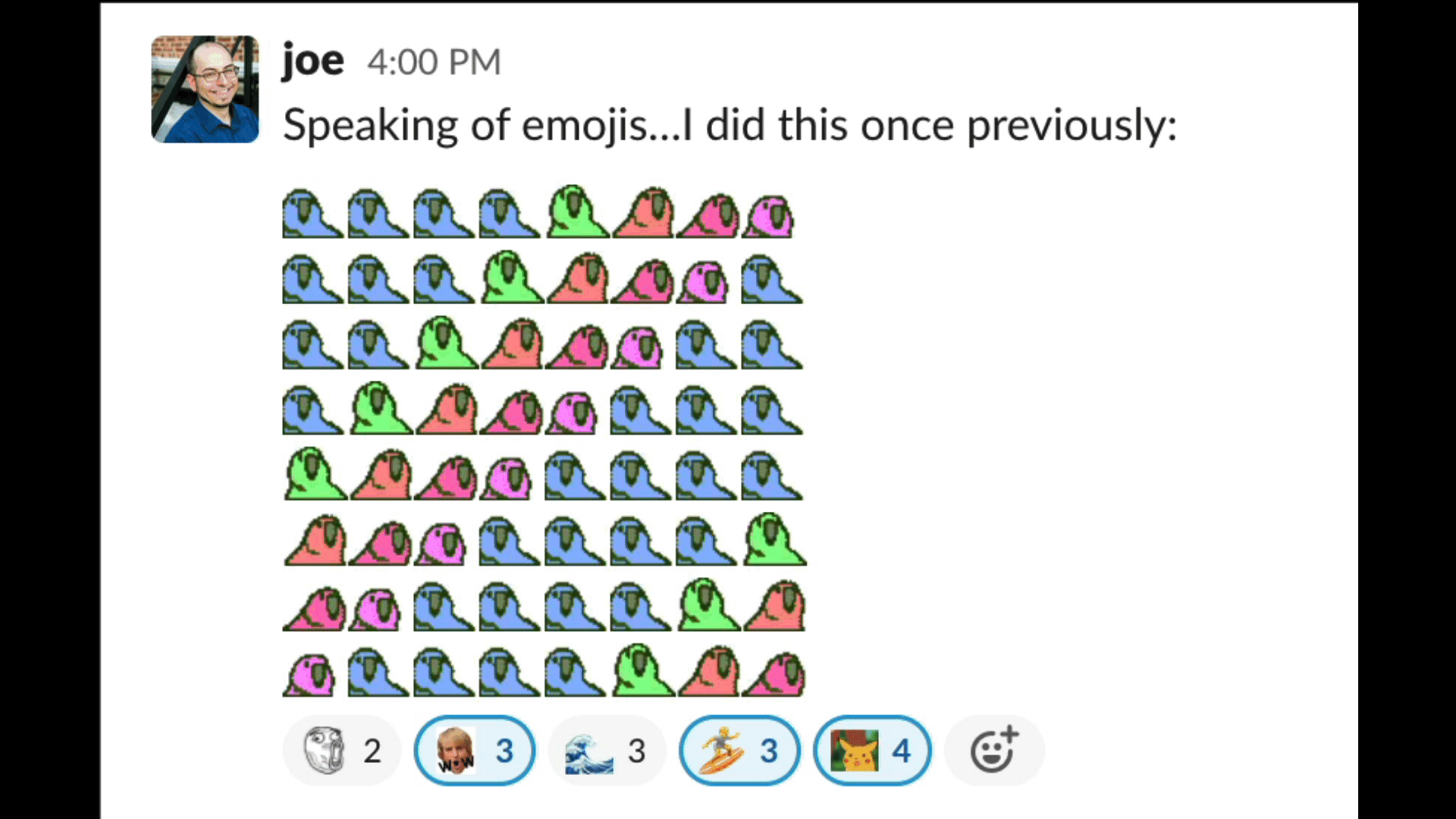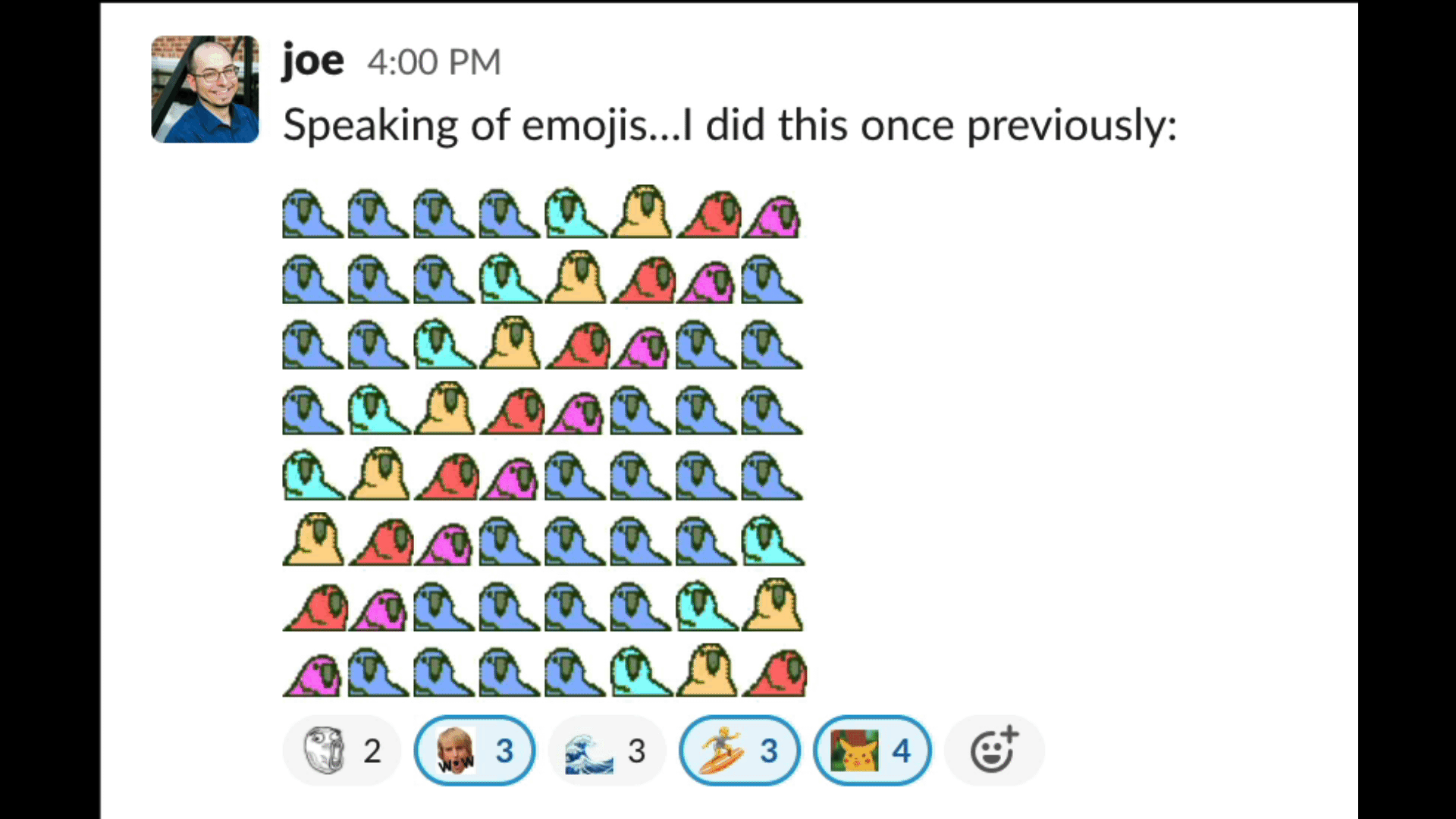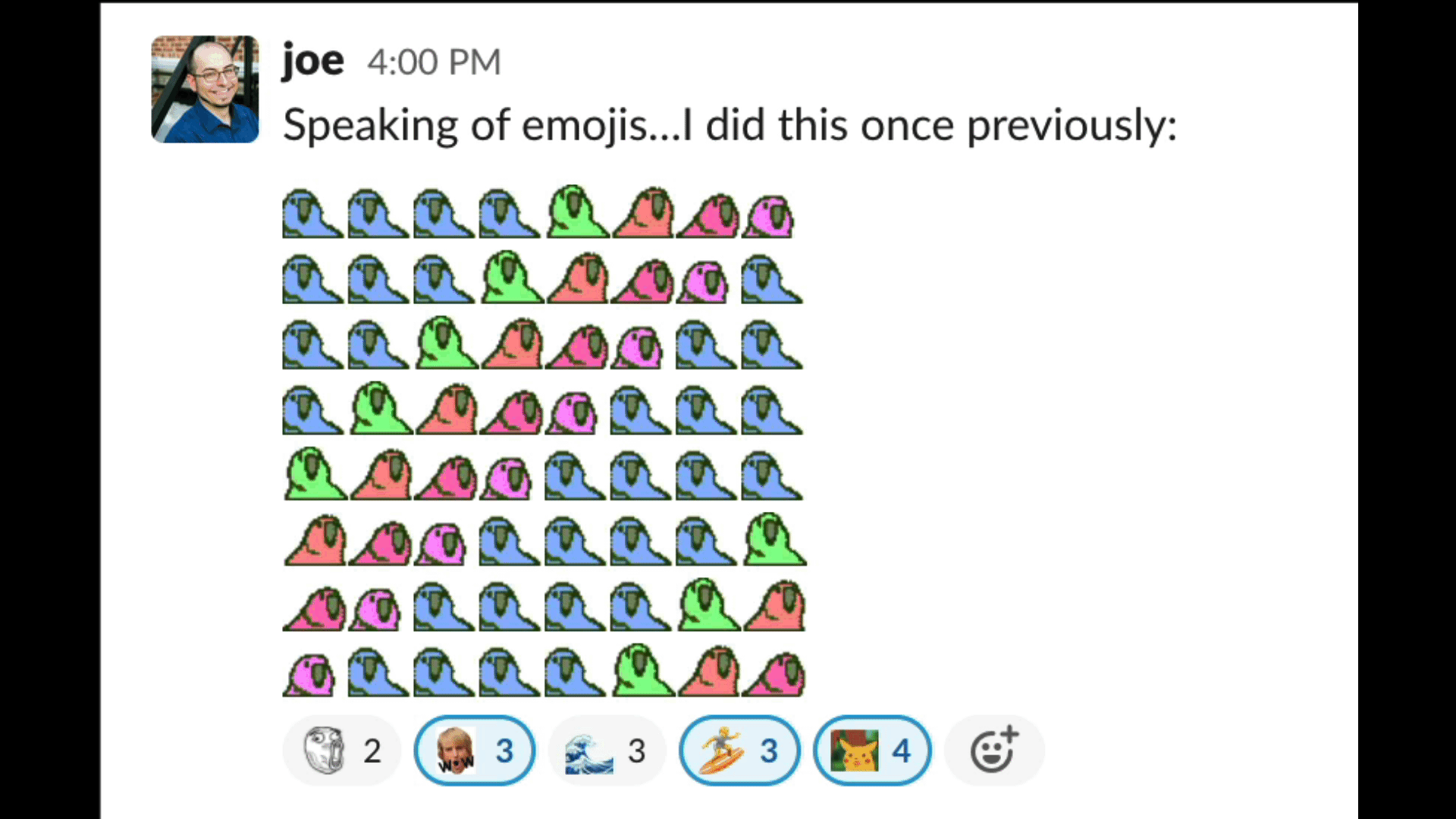
It’s a fun problem to think on: given some set of (successively delayed) party parrot emojis — say :wave1parrot:, :wave2parrot:, …, :wave8parrot: — , write a snippet to generate an 8×8 square of them doing the wave.

That is, write a script with the following output:

(Gist permalink.)

(…now’s your chance to draft an approach before the spoiler below.)

(Padding.)

(Padding.)

(Padding.)

(Padding.)

Here’s what I came up with in Swift:

(Gist permalink.)

The parrotEmojis[$0...] + parrotEmojis[..<$0] pivoting on the fifth line stuck with me — it’s a trick I borrowed from Leo Dabus’ Stack Overflow answer on Array rotations.

Which got me wondering, does the Standard Library provide an affordance for rotating its hierarchy of Collection protocols?

Turns out the Standard Library itself doesn’t, yet the swift-algorithms package has us covered (the real MVP) with a mutating variant under the MutableCollection.rotate(toStartAt:) method name. While we could modify the package’s implementation to be non-mutating, I wanted to see how broadly we could apply the someCollection[$0...] + someCollection[..<$0] approach across the Collection protocols.

Range subscripting is defined on Collection, returning a Subsequence, so we can start there (subbing in AnyCollection<Element> for the return type, which we’ll address next).

(Gist permalink.)

The second error points to the RangeReplaceableCollection overload of +(_:_:) being selected, which means we can quickly resolve the compilation error by following its guidance and returning a Subsequence out (since concatenating two Subsequences yields a Subsequence).

(Gist permalink.)

The extension Collection where SubSequence: RangeReplaceableCollection { /* … */ } constraint is worth pausing on. Are there any Collections out there whose subsequences are range-replaceable (RR, for short), yet the parent collection isn’t? I asked some folks over in an iOS Slack and Tim Vermeulen reminded me that since self[...] is a subsequence of the entire collection, any collection with RR subsequences can be made RR itself “by delegating all RR logic to self[...].”

You could in theory create your own non-RR collection type for which the subsequence is RR, but it’s guaranteed that there exist no cases of this because such a base collection always can be RR by delegating all RR logic to self[...].

— Tim V.

Which means the extension’s constraint is functionally equivalent to extending RangeReplaceableCollection itself.

(Gist permalink.)

⬦

I could’ve called it here, but there was a note in swift-algorithm’s docs. that got me wondering even further.

[In Ruby,] you can rotate the elements of an array by a number of positions, either forward or backward (by passing a negative number).

So, let’s try to write a rotated(by:) overload, shall we?

To start, the following equality should hold (if we assume positive bys rotate to the left and negative, to the right):

let oneTwoThree = [1, 2, 3]
oneTwoThree.rotated(by: -1) ==
  oneTwoThree.rotated(by: oneTwoThree.count - 1) // ⇒ `true`

The -1 to oneTwoThree.count - 1 wraparound hints at our old pal, the modulus operator. Maybe we can modulo out the by parameter and mirror rotated(toStartAt:) above (with an empty collection check for safe measure)?

(Gist permalink.)

Taking a test drive with the oneTwoThree example above…crashes…?

let oneTwoThree = [1, 2, 3]
oneTwoThree.rotated(by: -1) == // ❌ “Fatal error: Negative `Array` index is out of range.”
  oneTwoThree.rotated(by: oneTwoThree.count - 1) // ⇒ `true`

Hmmm, weird, that means the shiftPoint calculation — -1 % 3 — is -1? Usually modulo $n$ operations land squarely in $\left[0, n\right)$ (excluded on the right). %’s docs. call out why this happens:

The result of the remainder operator has the same sign as lhs [(-1 in our example)] and has a magnitude less than rhs.magnitude.

Alas. The more mathematical form of the operator was pitched (and even considered) on the Swift Forums before the thread lost steam back in July ’18. Still, it linked out to Rust’s RFC for their analog that I translated into Swift.

(Gist permalink.)

With that, the oneTwoThree example is back in non-crashing order and we can finally re-work the original party parrot wave.

let parrotEmojis = (1...8).map { ":wave\($0)parrot:" }

parrotEmojis.indices
  .map { parrotEmojis.rotated(by: $0).joined() }
  .joined(separator: "\n")

⬦

I’ll stop here because I didn’t imagine I’d write — checks word count — 650+ words on rotating Party Parrot emojis. I gotta admit though, entries like this have been my favorites as of late.

Please reach out if you have another approach! A good friend John Feminella mentioned that there might be a way to “exploit the square symmetry somehow.” That is,

…by “exploit,” I mean that you are making a row of $N$ things, $N$ times, where the $i$th row is rotated by $i$ elements, so instead of making it once and rotating $N$ times, you could just make it $N$ times.

— John F.

Consider this an exercise for the dedicated reader.