Getting an intuition around why we can call contramap a pullback

17 Oct 2019 ⇐ Notes archive

(This is an entry in my technical notebook. There will likely be typos, mistakes, or wider logical leaps — the intent here is to “let others look over my shoulder while I figure things out.”)

---

Last October, Brandon and Stephen reintroduced contramap—covered in episode 14—as pullback.

(The analog for the Haskell peeps is Contravariant’s contramap requirement.)

However, the name contramap isn’t fantastic. In one way it’s nice because it is indeed the contravariant version of map. It has basically the same shape as map, it’s just that the arrow flips the other direction. Even so, the term may seem a little overly-jargony and may turn people off to the idea entirely, and that would be a real shame.

Luckily, there’s a concept in math that is far more general than the idea of contravariance, and in the case of functions is precisely contramap. And even better it has a great name. It’s called the pullback. Intuitively it expresses the idea of pulling a structure back along a function to another structure.

—“Some news about contramap”

I had trouble getting an intuition around why contramap’ing is a pullback, in the categorical sense and here’s why (mirroring a recent Twitter thread):

@pointfreeco—Hey y’all 👋🏽 I’m a tad confused when it comes to grounding the canonical pullback diagram with types and functions between them. (Pardon the rough sketch hah, I forgot my LaTeX and this was more fun. 😄) /1

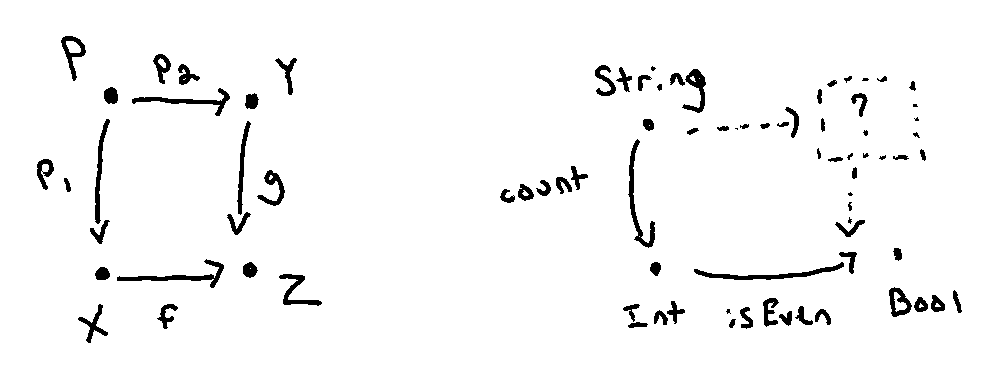
Pullbacks, generally, seem to give two morphisms and objects worth of freedom—f, g, X, and Y—whereas in code, we almost always seem to pullback along one [path across] the square. /2

Do y’all call this operation pullback because there isn’t a restriction preventing f from equaling g and X equaling Y (collapsing the square into a linear diagram)? /3

Yesterday, Eureka Zhu cleared up my confusion on why we don’t take the upper path through pullback’s definitional diagram:

In [the] Set [category], the pullback of f: a -> c along g: b -> c is { (a, b) | f a = g b }, which is sometimes undecidable in Haskell [and by extension, Swift].

Hand-waving past Hask and Swift not quite being categories, we reason about them through the category Set.

And Zhu points out that a pullback in Set requires us to equate two functions, f and g in the diagram above, for a subset of inputs and that’s undecidable in programming.

How do we get around this?

Well, setting X to be Y and f to g:

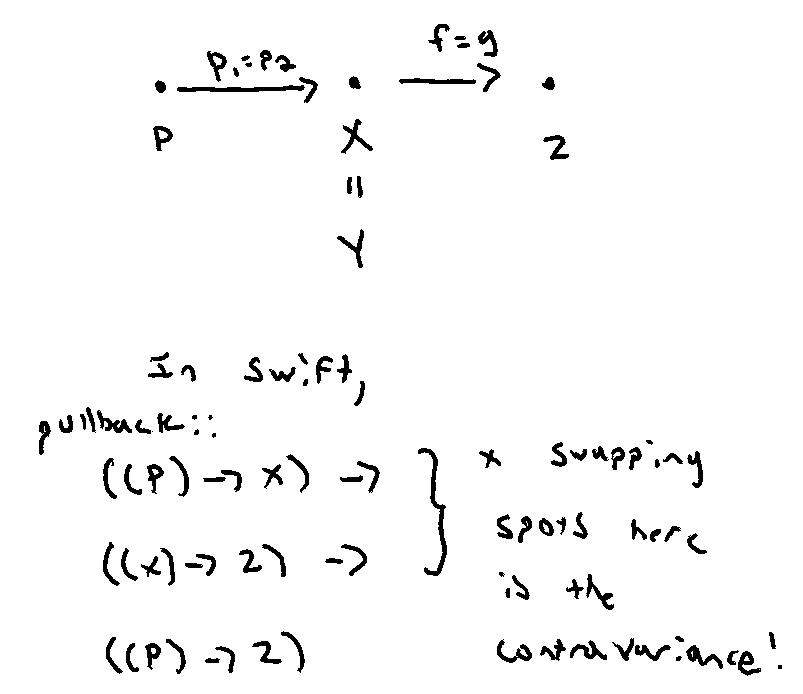
Since pure functions equal themselves, we can sidestep that undecidability by collapsing the diagram. Wickedly clever.

That’s how pullback’s flexibility allows us to consider contramap as a specialization of it.