Distillations About

What makes natural transformations, natural?

19 Oct 2019 ⇐ Notes archive

(This is an entry in my technical notebook. There will likely be typos, mistakes, or wider logical leaps — the intent here is to “let others look over my shoulder while I figure things out.”)

Learning category theory often involves patiently sitting with a concept until it—eventually—clicks and then considering it as a building block for the next1.

Grokking natural transformations went that way for me.

I still remember the team lunch last spring where I couldn’t keep my excitement for the abstraction a secret and had to share with everyone (I’m a blast at parties).

After mentioning the often-cited example of a natural transformation in engineering, Collection.first (a transformation between the Collection and Optional functors), a teammate asked me the question heading this note:

What makes a natural transformation, natural?

I found an interpretation of the word.

Say we have some categories C and D and functors F and G between them, diagrammed below:

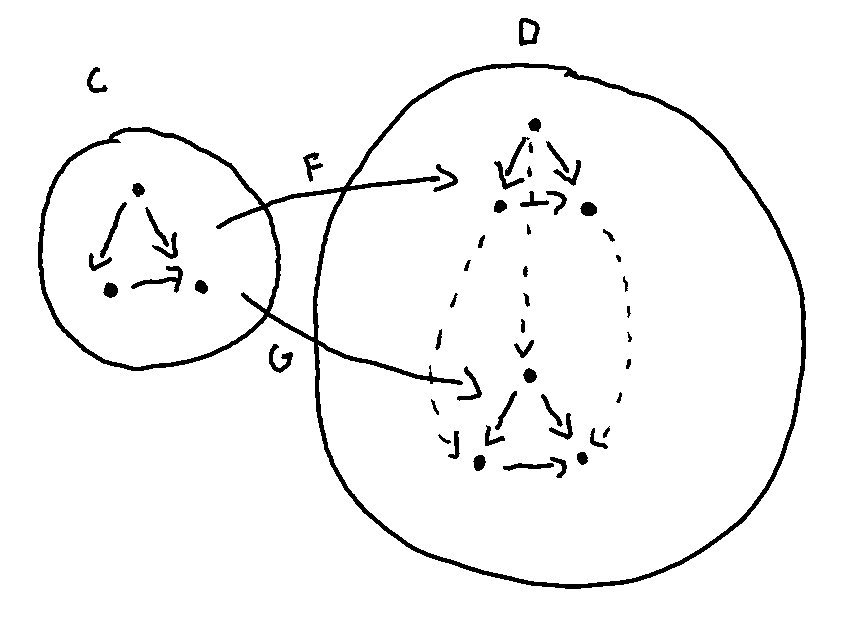
If we wanted to move from the image of F acting on C to the image of G, we have to find a way of moving between objects in the same category.

The question, rephrased, becomes what connects objects in a category? Well, morphisms!

Now, how do we pick them? Another condition on natural transformations is that the square formed by mapping two objects, A and B connected by a morphism f, across two functors F and G must commute.

Let’s call our choices of morphisms between F_A and G_A and F_B and G_B, α_A and α_B, respectively.

Even if f flips directions across F and G—i.e. they’re contravariant functors—our choice in α_A and α_B is fixed!

The definition, the choice of morphisms, seems to naturally follow from structure at hand. It doesn’t depend on arbitrary choices.

Tangentially, a definition shaking out from some structure reminds me of how the Curry–Howard correspondence causes certain functions to have a unique implementation. Brandon covered this topic in a past Brooklyn Swift presentation (timestamped).

For more resources on natural transformations:

  1. Then, repeating further. One day, I hope to have built the machinery needed to read Riehl’s research and writing on ∞-category theory. ↩