Naturality condition

01 Nov 2019 ⇐ Notes archive

(This is an entry in my technical notebook. There will likely be typos, mistakes, or wider logical leaps — the intent here is to “let others look over my shoulder while I figure things out.”)

---

I’m currently working through Mio Alter’s post, “Yoneda, Currying, and Fusion” (his other piece on equivalence relations is equally stellar).

Early on, Mio mentions:

It turns out that being a natural transformation is hard: the commutative diagram that a natural transformation has to satisfy means that the components […] fit together in the right way.

Visually, the diagram formed by functors F and G between C and D and with natural transformation α must commute (signaled by the rounded arrow in the center).

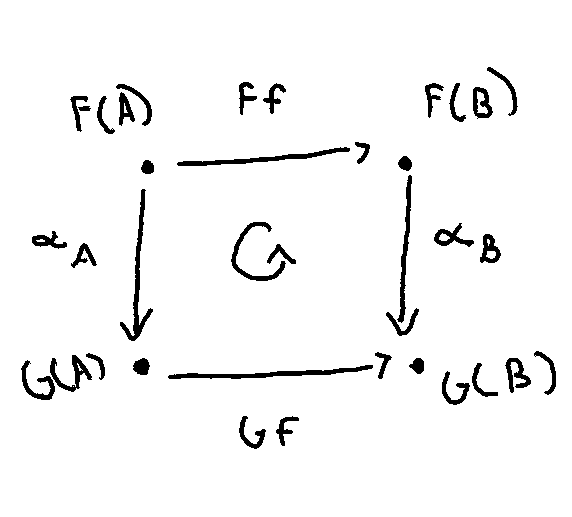
I’m trying to get a sense for why this condition is “hard” to meet.

What’s helped is making the commutativity explicit by drawing the diagonals and seeing that they must be the equal. The four legs of the two triangles that cut the square must share a common diagonal.

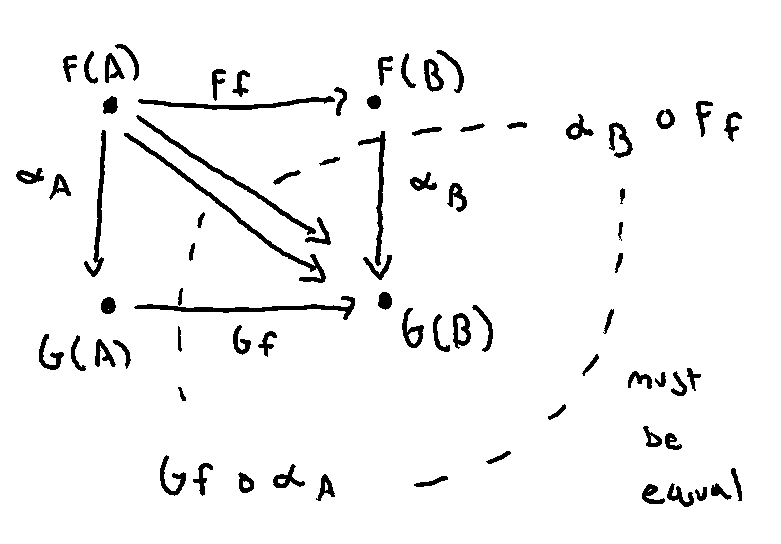
Maybe that’s why natural transformations are rare? There might be many morphisms between F(A) and G(A) and F(B) and G(B), but only a select few (or none) which cause their compositions to coincide.

For more on commutative diagrams, Tai-Danae Bradley has a post dedicated to the topic.