Profunctors generalize relations
25 Apr 2020 ⇐ Notes archive(This is an entry in my technical notebook. There will likely be typos, mistakes, or wider logical leaps — the intent here is to “let others look over my shoulder while I figure things out.”)
An aside before the note, Day One reminded me that I started studying category theory, in earnest, almost a year ago today.
Despite being a hobby, I’m pretty proud of how far I’ve come (I struggle with saying that aloud, since I’m the type to keep pushing forward and not really look around along the way).
I’m
- in a research group,
- followed along and typeset solutions for Programming with Categories,
- shot my shot and applied to Adjoint School and Causeway (got rejected from the former and the latter got cancelled—still, I tried),
- and am learning from and met incredibly kind folks like Jade, Sarah, and Jeremy.
Richard Guy put how I’ve felt as of late succinctly.
…and I love anybody who can [do mathematics] well, so I just like to hang on and try to copy them as best I can, even though I’m not really in their league.
(I’m not sure if anyone reads these entries hah (quite literally, I removed analytics on the site a few years ago). If so, pardon the moment to reflect.)
⬦
I was revisiting profunctors yesterday and Bartosz mentioned an intuition in lecture III.6.1 (timestamped) that made their motivation click.
You can think of a profunctor as [generalizing] a relation between objects.
Huh, okay. Let’s take a step back and recap what a relation is in plain ol’ set theory and follow the intuition.
A binary relation over two sets $X$ and $Y$ is a subset of their Cartesian product, $X \times Y$. That is, a set of ordered pairs indicating which $X$s are related to specific $Y$s.
And now to generalize.
First, let’s swap out the sets for categories $C$ and $D$.
$C \times D$. Okay, the product category. Since $C$ and $D$ are possibly distinct categories, we can’t directly consider morphisms between them. But, we can in their product category—morphisms between objects $(c, d)$ and $(c^\prime, d^\prime)$ are those in the form $(f, g)$ with $f: c \rightarrow c^\prime$ and $g: d \rightarrow d^\prime$. So, in a sense, the collection of relationships between $c$ and $d$ is $\textrm{Hom}((c, d), (c^\prime, d^\prime))$.
That hom-set is, well, a set (assuming we’re working with small categories)! What if we tried to create a functor from $C \times D \rightarrow \mathbf{Set}$ defined by $(c, d) \mapsto \ldots$
Wait. $c$ and $d$ come from different categories and hom-sets only work in a single category. I read around to reconcile this and stumbled upon heteromorphisms. “Morphisms” between two objects from different categories that use a bridging functor to then construct a hom-set. I got lost trying to read further, and with warning from slide 3/41 of David Ellerman’s presentation on the topic.
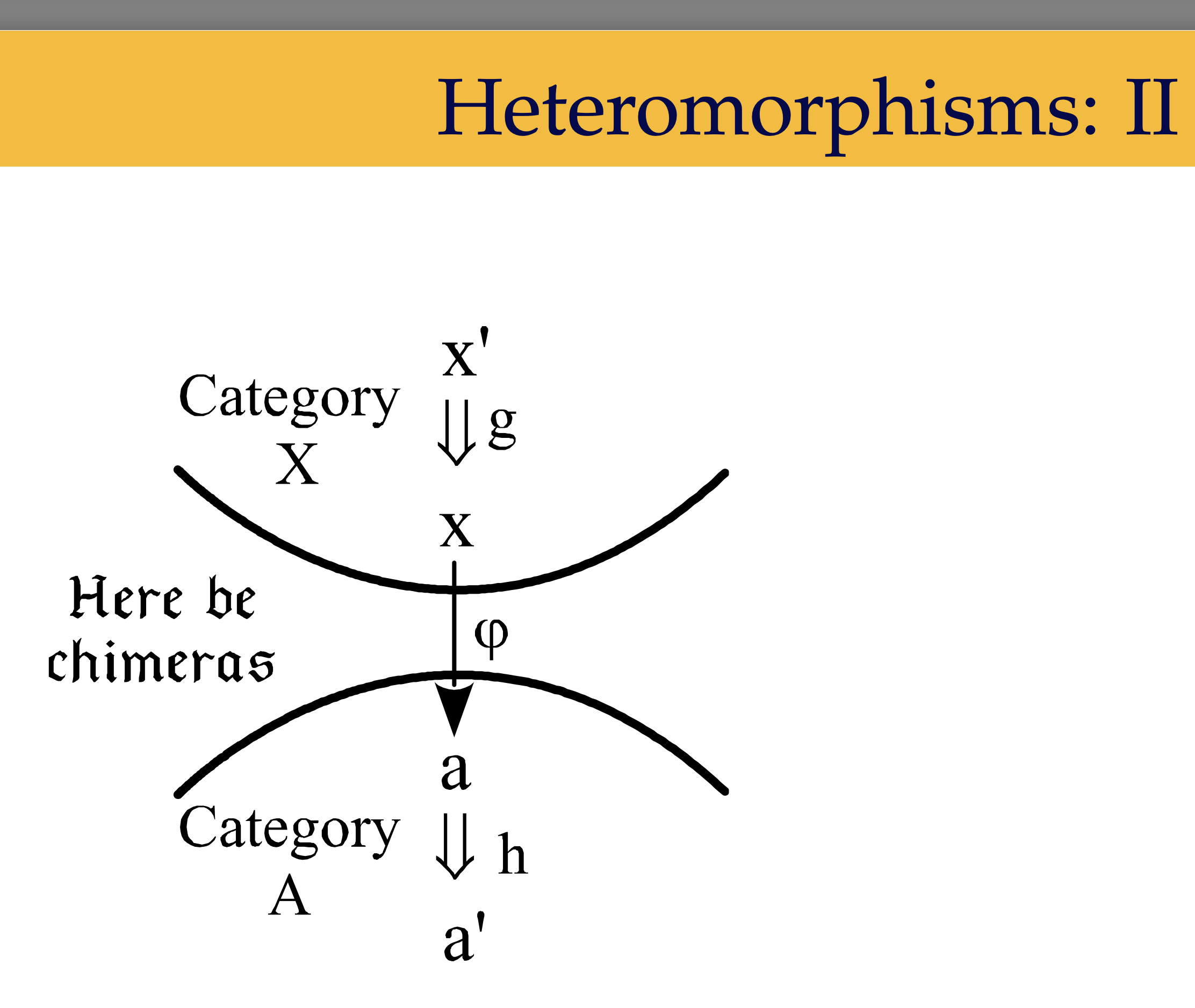
So, let’s assume $C = D$ and carry on (I’ll understand that presentation someday).
Okay, let’s map $c, d$ (both objects in $C$) to $\textrm{Hom}(c, d)$. And for morphisms, we need to map some $(f, g)$ for $f: c \rightarrow c^\prime$ and $g: d \rightarrow d^\prime$ to a function between $\textrm{Hom}(c, d)$ and $\textrm{Hom}(c^\prime, d^\prime)$. Let’s pluck out a morphism, say $h$ from $\textrm{Hom}(c, d)$.
We have $f, g, h$ in hand and need to construct a morphism from $c^\prime$ to $d^\prime$. There’s…no way to do this. None of our morphisms map from $c^\prime$.
That’s where the contravariance in the profunctor construction comes from when folks write $C^{\textrm{op}} \times C \rightarrow \mathbf{Set}$ (or, in the general case $C^{\textrm{op}} \times D \rightarrow \mathbf{Set}$). Taking the dual in the first component of the product category flips $f$ and now lets us get from $c^\prime$ to $d^\prime$ by way of $g \circ h \circ f$.
It’s okay if you need to walk around the park with that composition before it makes sense. I certainly needed to and it demystified the rogue dimap’s I’d see in Preludes.
But, let’s take stock on how this generalizes relations. In the same-category setting, we’re constructing a functor that maps two objects to the ways in which they’re related, their hom-sets. Since it’s a functor, we also need to consider mapping morphisms across the functor into functions between hom-sets and dimap (link to Haskell’s Prelude) does just that.