Notebook Archive

(Note: these are entries from my technical notebook. There will likely be typos, mistakes, or wider logical leaps — the intent here is to “let others look over my shoulder while I figure things out.”)

A bug with Swift shorthand arguments

20 Feb 2022 A common kickflip in The Browser Company’s codebase is merging two dictionaries. Take two groups of tabs, each keyed on tab IDs with a corresponding Tab instance for values.

(Gist permalink.)

When merging tabGroup1 and tabGroup2, we need to consider the possibility — albeit rare with UUIDs — of key collisions. Do we unique duplicate keys with an existing value in the dictionary? Overwrite it? Or compute some new value based on the two? Thankfully Swift provides an affordance to handle this with Dictionary.merging(_:uniquingKeysWith:)¹.

Since computing a new value for duplicate keys doesn’t quite make sense here, let’s try both keeping existing and overwriting values wholesale.

(Gist permalink.)

And that’s the note’s title bug in action. When using shorthand names, the last argument must be referenced or you have to fall back to naming or ignoring every argument (i.e. { first, _ in first } above).

The bug has been outstanding for six years (!) and folks like John McCall described it as an issue “several people have made efforts to fix” and “it’s not easy.” Yet, there was a call for next steps in a thread David James revived just last month.

Two implementations of delaySubscription

17 Apr 2021 Jack Stone’s proposal and implementation of Publisher.delaySubscription was a TIL for me. I also didn’t know there was prior art for the operator in Rx.

It’s different than Publisher.delay in that it shifts the point of subscription forward in time instead of emissions (à la delay).

The primary step is holding a received subscription for the specified delay before forwarding it downstream. Which begs my favorite question, can this be implemented as composed operator? It can! An approach is tucked away in isowords’ repo under the Effect.deferred naming, where the Point-Free team uses it delay a Never-Never sound effect until after a game cube is removed.

Free variables in TCA dependencies

11 Apr 2021

Updates:

4/17/21:

Friend of the blog, Danny Hertz, brought up a good point: “one thing I’m curious about is how they make sure those globals are mutated on same thread.” Brandon replied with “it’s the responsibility of whoever makes the client — every spot dependencies is referenced, we know it’s on the main queue and if it wasn’t that’d be our error.”

TCA completely rewired how I think about dependencies (and, well, how non-TCA code I wrote in the past worked with so much implicit state). A loose end in my understanding of the designing dependencies series has been those mutable free variables hanging out alongside for cancellation handling. e.g. dependencies here in the SpeechRecognition case study (or at the bottom of the abbreviated version, below).

(Gist permalink.)

Van (a regular study group pal) and I paused with the lifecycle of this variable — is it initialized on app. launch? Lazily loaded?

The Swift Programming Language book had our back with the answer in the Properties section of the Language Guide chapter:

Global constants and variables are always computed lazily, in a similar manner to lazy stored properties. Unlike lazy stored properties, global constants and variables do not need to be marked with the lazy modifier.

Aha! So, dependencies is initialized as needed, even without a lazy tacked on. TIL!

withLatestFrom as a composed operator

10 Apr 2021 I kind of took CombineExt’s — and the ReactiveX specification of — Publisher.withLatestFrom for granted. “It probably subscribes to both upstream and the provided sequence, suspending output from upstream until the other emits, and subsequently forwards the latest values down from the latter when the former emits” was my reading of the filled out Publisher conformance. Which made me assume this dance wasn’t possible as a composed operator.

And the other day Ian showed me the way.

Here’s a sketch of the approach (with a selector variant):

(Gist permalink.)

If this isn’t the Combine equivalent of a kickflip — I don’t know what is.

The implicit capture of the upstream self in the other.map { … } closure is worth checking in on. Maybe we can write AnyObject-constrained overloads that weakly capture class-bound publishers? Turns out all but three conformances in the Publishers namespace are structs¹, so let’s account for those.

(Gist permalink.)

What’s wild is, at this point, we can sub in this implementation for CombineExt’s and the test suite still passes (!). Let’s check our work when it comes to terminal events, though.

Failures?

Failure events from either upstream or other are propagated down. Check.

(Gist permalink.)

Completions? This event type isn’t as intuitive. Should the argument’s completions be forwarded downstream? Let’s import CombineExt to see how the non-composed implementation handles this.

(Gist permalink.)

Hmm, alright, I can buy that second’s completions shouldn’t be sent downstream since withLatestFrom is essentially polling it for value events, caching the latest.

Now let’s nix the CombineExt import and see how our operator handles this.

(Gist permalink.)

…neither scenario completes? Oof — and this checks out because the implementation’s map-switchToLatest dance only completes when upstream and all of the projected sequences complete² (i.e. the scenarios in the snippet finish if you tack on first.send(completion: .finished) and second.send(completion: .finished) to each, respectively).

But wait, didn’t Ext’s test suite pass with this implementation? It did, because at the time of writing (commit 8a070de) every test case in WithLatestFromTests.swift checks for withLatestFrom’s completion only after every argument and upstream has completed (missing the cases where only upstream finishes or the arguments do, but not both).

Here’s Rx’s handling of the parenthesized cases:

(Gist permalink.)

Back to the drawing board.

To recap, our implementation handles value and error events to spec. and needs to be reworked to finish when upstream does, even if the operator’s argument doesn’t.

We can pull this off by using a note I wrote about on Publisher.zip completions — specifically, that if any one of the publishers in a zip completes, the entire zipped sequence completes.

(Gist permalink.)

Which begs the question, if our initial, non-zipped implementation passes CombineExt’s test suite? Does its implementation handle lone upstream completions? Let’s add a test case and take a look:

(Gist permalink.)

Shoot. Ext’s implementation doesn’t handle this.

So, we have two options: either rework Ext to handle this case or sub in our composed variant which does. To kick off the discussion, I wrote an issue over at CombineCommunity/CombineExt/87 with a sketch of how a PR for the latter approach could look.

⬦

The tl;dr is it’s possible to pull off Publisher.withLatestFrom as a composed operator! And while a full Publisher conformance can be more idiomatic, it’s fun to think on what it means to factor the operator’s behavior into the composition of ones that ship with the framework.³

Iverson brackets and SwiftUI modifiers

21 Mar 2021 I love noticing when an everyday engineering practice has a named analog in mathematics. This time around, it was Iverson brackets. The Wikipedia page is…a lot, so no frets if it’s intimidating — the non-mathematician’s reading of it is the expression $[P]$ is equal to $1$ if $P$ is true or $0$, if false, where $P$ is some predicatetrue-false statement.

In Swift speak, a function from Bool to Int¹.

In SwiftUI speak, conditionally setting a modifier’s value². Most commonly with opacity(_:),

someView.opacity(isShown ? 1 : 0).

And implicitly with others like rotationEffect(_:anchor:),

someView
  .rotationEffect(.degrees(isRotated ? 90 : 0))

// which expands out to,

someView
  .rotationEffect(.degrees(90 * (isRotated ? 1 : 0)))

The isShown ? 1 : 0 and isRotated ? 1 : 0 ternaries are Iverson brackets in disguise. Kinda nifty to see another domain’s language around this type of expression. I came across the notation in an answer to the question of “What is the sum of number of digits of the numbers $2^{2001}$ and $5^{2001}$?” asked over on Math Stack Exchange.

The next note will likely pencil in the intermediary steps of that solution.

Party Parrot waves and Collection rotations

14 Mar 2021

Updates:

3/14/21:

Soroush messaged that using RangeReplaceableCollection’s + overload unfortunately incurs a copy. I’ve added a footnote¹ with his workaround that coincidentally uses John’s hint at the end about leaning on the square’s symmetry across the diagonal.

Joe Spadafora sent an emoji masterpiece in our team’s Slack the other day that doubled as a code golf.

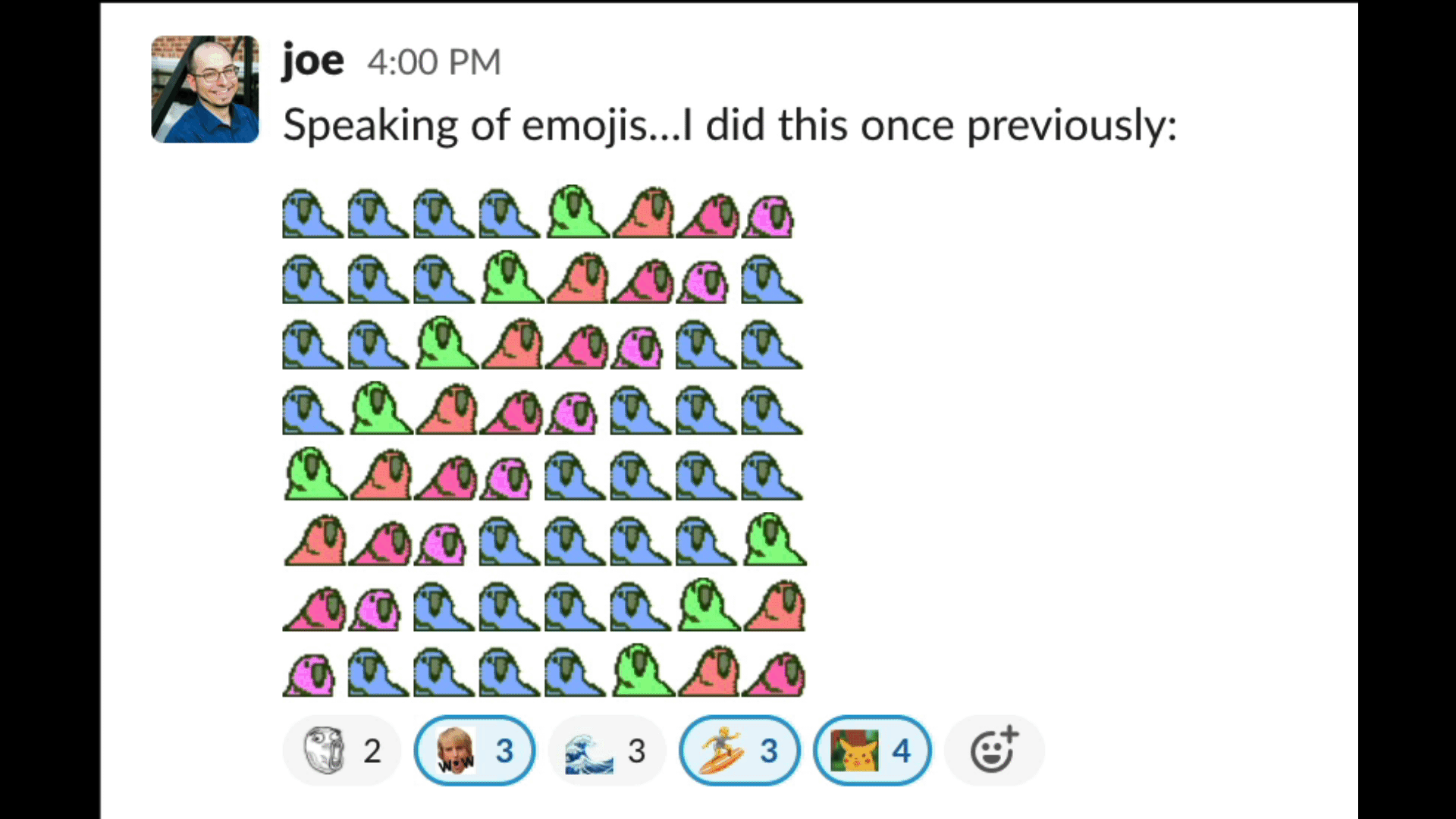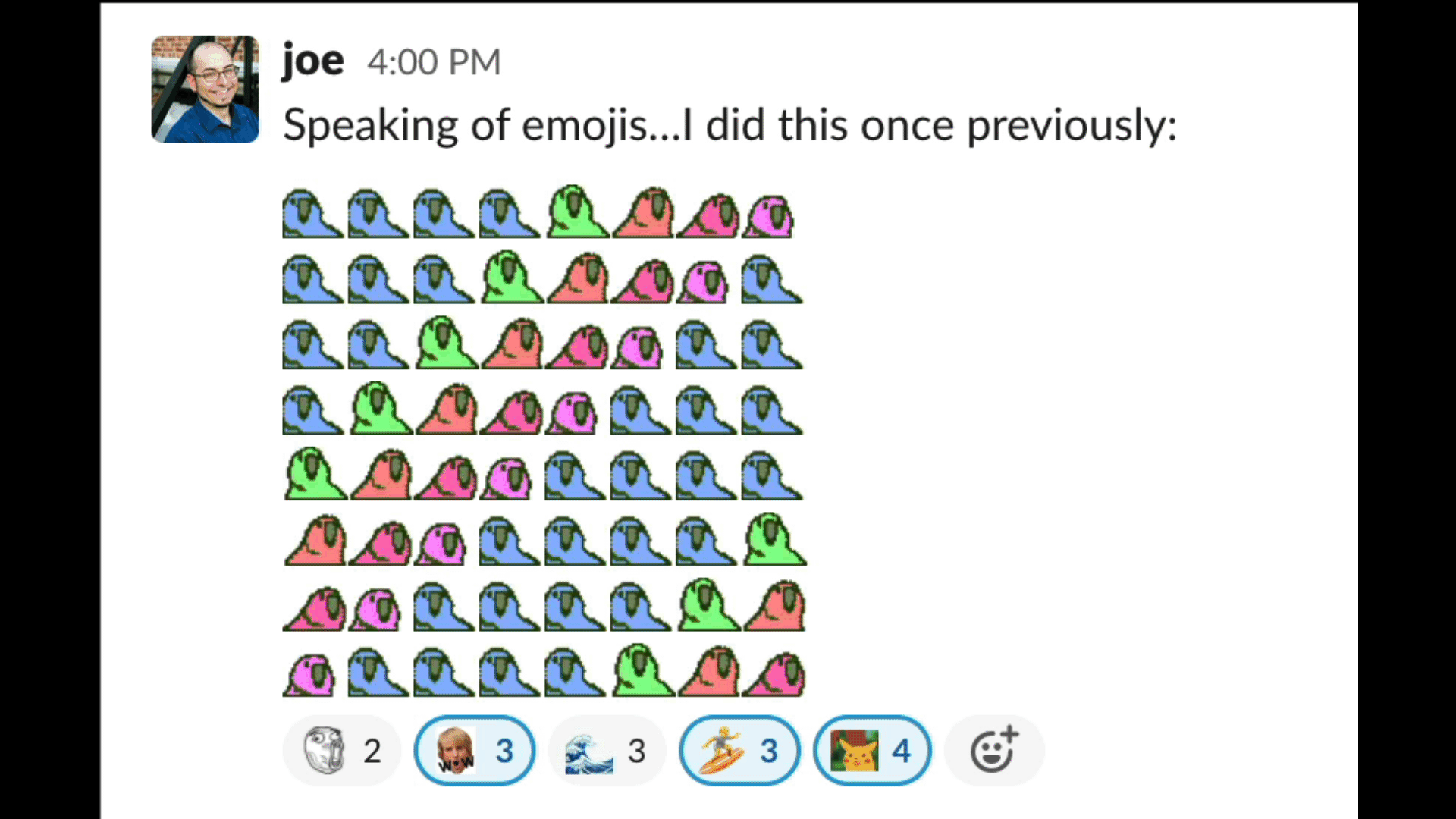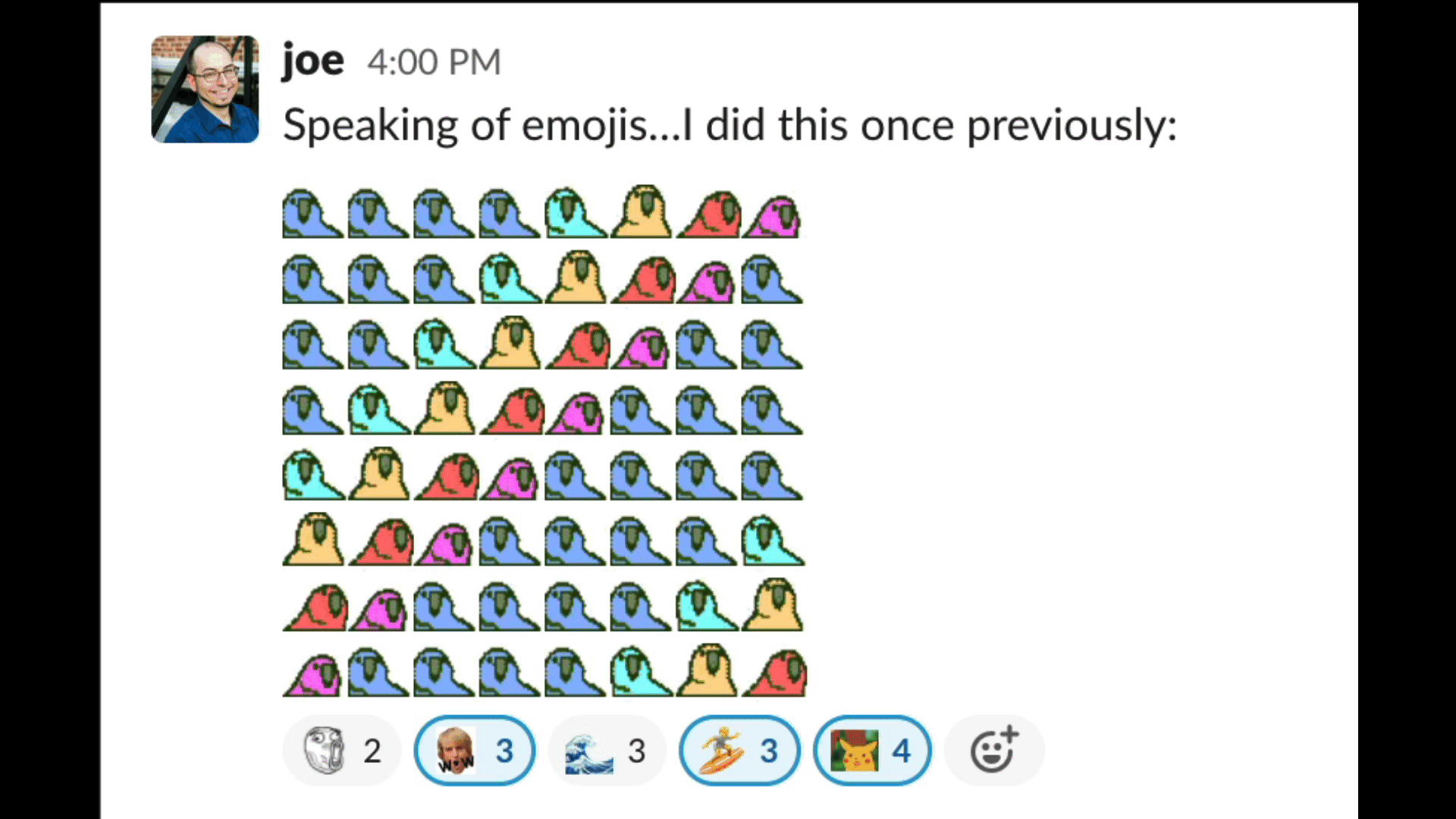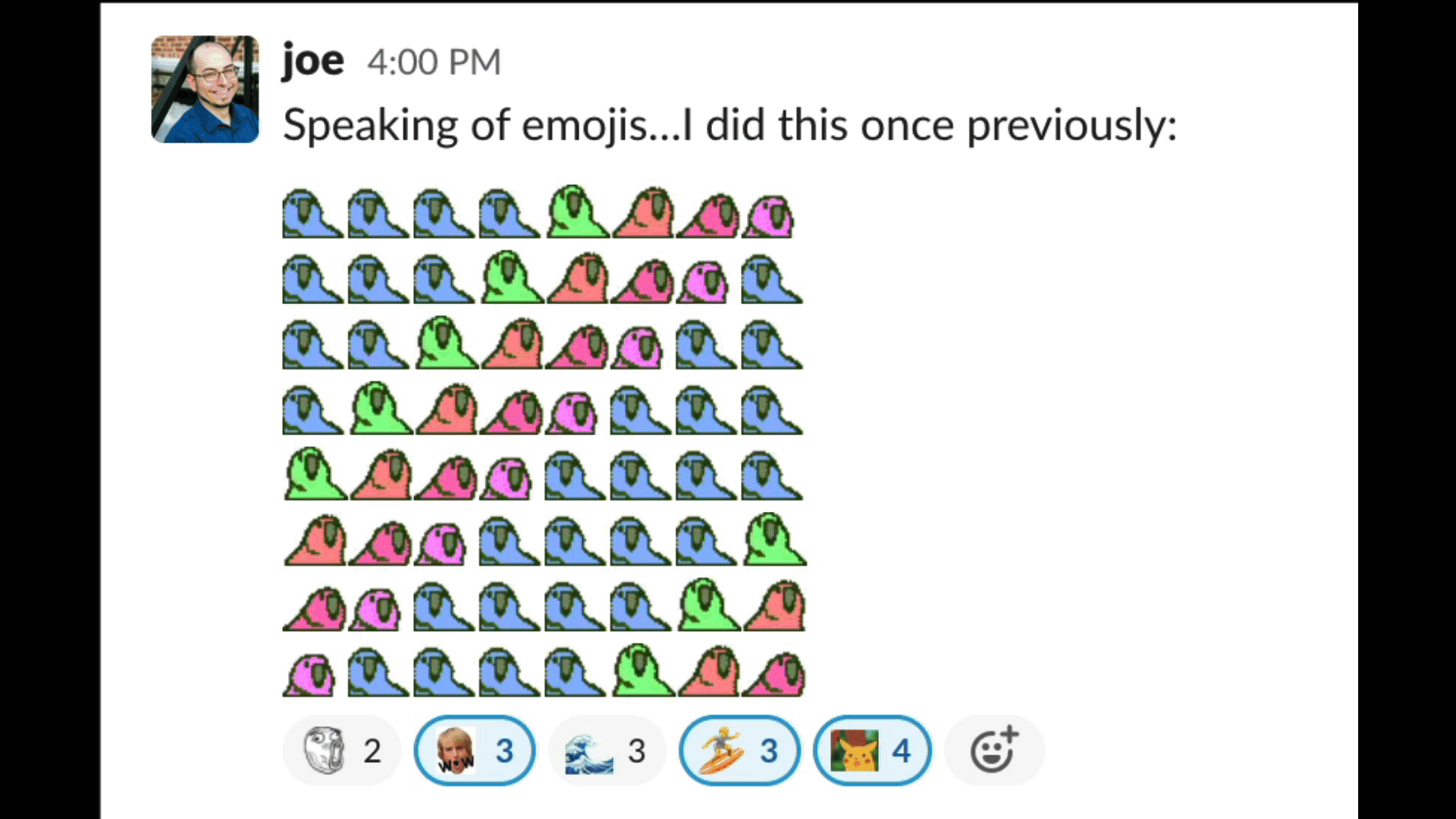
It’s a fun problem to think on: given some set of (successively delayed) party parrot emojis — say :wave1parrot:, :wave2parrot:, …, :wave8parrot: — , write a snippet to generate an 8×8 square of them doing the wave.

That is, write a script with the following output:

(Gist permalink.)

(…now’s your chance to draft an approach before the spoiler below.)

(Padding.)

(Padding.)

(Padding.)

(Padding.)

Here’s what I came up with in Swift:

(Gist permalink.)

The parrotEmojis[$0...] + parrotEmojis[..<$0] pivoting on the fifth line stuck with me — it’s a trick I borrowed from Leo Dabus’ Stack Overflow answer on Array rotations.

Which got me wondering, does the Standard Library provide an affordance for rotating its hierarchy of Collection protocols?

Turns out the Standard Library itself doesn’t, yet the swift-algorithms package has us covered (the real MVP) with a mutating variant under the MutableCollection.rotate(toStartAt:) method name. While we could modify the package’s implementation to be non-mutating, I wanted to see how broadly we could apply the someCollection[$0...] + someCollection[..<$0] approach across the Collection protocols.

Range subscripting is defined on Collection, returning a Subsequence, so we can start there (subbing in AnyCollection<Element> for the return type, which we’ll address next).

(Gist permalink.)

The second error points to the RangeReplaceableCollection overload of +(_:_:) being selected, which means we can quickly resolve the compilation error by following its guidance and returning a Subsequence out (since concatenating two Subsequences yields a Subsequence).

(Gist permalink.)

The extension Collection where SubSequence: RangeReplaceableCollection { /* … */ } constraint is worth pausing on. Are there any Collections out there whose subsequences are range-replaceable (RR, for short), yet the parent collection isn’t? I asked some folks over in an iOS Slack and Tim Vermeulen reminded me that since self[...] is a subsequence of the entire collection, any collection with RR subsequences can be made RR itself “by delegating all RR logic to self[...].”

You could in theory create your own non-RR collection type for which the subsequence is RR, but it’s guaranteed that there exist no cases of this because such a base collection always can be RR by delegating all RR logic to self[...].

— Tim V.

Which means the extension’s constraint is functionally equivalent to extending RangeReplaceableCollection itself.

(Gist permalink.)

⬦

I could’ve called it here, but there was a note in swift-algorithm’s docs. that got me wondering even further.

[In Ruby,] you can rotate the elements of an array by a number of positions, either forward or backward (by passing a negative number).

So, let’s try to write a rotated(by:) overload, shall we?

To start, the following equality should hold (if we assume positive bys rotate to the left and negative, to the right):

let oneTwoThree = [1, 2, 3]
oneTwoThree.rotated(by: -1) ==
  oneTwoThree.rotated(by: oneTwoThree.count - 1) // ⇒ `true`

The -1 to oneTwoThree.count - 1 wraparound hints at our old pal, the modulus operator. Maybe we can modulo out the by parameter and mirror rotated(toStartAt:) above (with an empty collection check for safe measure)?

(Gist permalink.)

Taking a test drive with the oneTwoThree example above…crashes…?

let oneTwoThree = [1, 2, 3]
oneTwoThree.rotated(by: -1) == // ❌ “Fatal error: Negative `Array` index is out of range.”
  oneTwoThree.rotated(by: oneTwoThree.count - 1) // ⇒ `true`

Hmmm, weird, that means the shiftPoint calculation — -1 % 3 — is -1? Usually modulo $n$ operations land squarely in $\left[0, n\right)$ (excluded on the right). %’s docs. call out why this happens:

The result of the remainder operator has the same sign as lhs [(-1 in our example)] and has a magnitude less than rhs.magnitude.

Alas. The more mathematical form of the operator was pitched (and even considered) on the Swift Forums before the thread lost steam back in July ’18. Still, it linked out to Rust’s RFC for their analog that I translated into Swift.

(Gist permalink.)

With that, the oneTwoThree example is back in non-crashing order and we can finally re-work the original party parrot wave.

let parrotEmojis = (1...8).map { ":wave\($0)parrot:" }

parrotEmojis.indices
  .map { parrotEmojis.rotated(by: $0).joined() }
  .joined(separator: "\n")

⬦

I’ll stop here because I didn’t imagine I’d write — checks word count — 650+ words on rotating Party Parrot emojis. I gotta admit though, entries like this have been my favorites as of late.

Please reach out if you have another approach! A good friend John Feminella mentioned that there might be a way to “exploit the square symmetry somehow.” That is,

…by “exploit,” I mean that you are making a row of $N$ things, $N$ times, where the $i$th row is rotated by $i$ elements, so instead of making it once and rotating $N$ times, you could just make it $N$ times.

— John F.

Consider this an exercise for the dedicated reader.

Implementing AnyEquatable

04 Mar 2021 Point-Free #133.1 is a hidden gem¹. Outside the episode’s FormAction BindingAction context, it asks the viewer to implement a type eraser on the Equatable protocol. Here’s a quick note on the implementation because I’m still thinking about how wicked it is a month later — first, some scaffolding we’ll work under.

struct AnyEquatable: Equatable {
  let value: // ???
  
  init<Value: Equatable>(_ value: Value) {
    self.value = // ???
  }
  
  static func == (lhs: AnyEquatable, rhs: AnyEquatable) -> Bool {
    // ???
  }
}

Presumably we’d want to expose AnyEquatable.value — but, we can’t make it of type Value, since that’d require threading the underlying generic at the type level, defeating the purpose of erasure in the first place. Maybe…Any? That’d further mean, ==’s implementation needs to remember value’s Value-ness if it has any hope of comparing it against rhs.value (since it’s another Any). So maybe we hold onto an Any-based predicate‽ It’s kinda wild, yet this seems to be the only implementation we can pull off sans compiler-generated magic like AnyHashable².

struct AnyEquatable: Equatable {
  let value: Any
  private let valueIsEqualTo: (Any) -> Bool

  init<Value: Equatable>(_ value: Value) {
    self.value = value
    valueIsEqualTo = { other in other as? Value == value }
  }

  static func == (lhs: AnyEquatable, rhs: AnyEquatable) -> Bool {
    lhs.valueIsEqualTo(rhs.value)
  }
}

(!).

Giving it a spin lets us mix and match erased values of the same or different underlying types.

AnyEquatable(5) == .init(4) // ⇒ false
AnyEquatable(5) == .init(5) // ⇒ true
AnyEquatable(5) == .init("Five") // ⇒ false

Er wait, hmm — I looked into why this isn’t already built into the language (à la AnyHashable) and it turns out this implementation breaks with classes and subclassing. Maybe TCA gets away with this since it’s recommended that the State graph be composed entirely of value types:

In general, we think that state needs to consist of simple value types, and as soon as you introduce classes and objects you expose yourself to a lot of undefined behavior […]. If you need parts of these classes in your state we recommend defining structs that hold just the value-based [representations].

The library also fences off misusing AnyEquatable by embedding value and valueIsEqualTo into BindingAction, directly.

And as a final tangent, SwiftUI prevents the similar problem of conforming reference types to View, ButtonStyle, et al by trigging runtime assertions.

Types conforming to any style protocol, such as ButtonStyle, ToggleStyle, are now enforced to be value types. Styles must be structures or enumerations, not classes, and conforming a class to a style protocol may trigger an assertion. This is the same restriction that the system has always enforced on types conforming to View. (62886135)

atan versus atan2

01 Mar 2021 I never really thought twice — let alone since high school pre-calculus — about the atan function (shorthand for arctangent)¹. And it wasn’t until Richard Borcherds pointed out the difference between atan and atan2 (the arity two form) in a recent complex analysis lecture, that I realized I also haven’t paused with why there’s two variants.

The two-argument form is needed because the single-argument function loses the individual signs (positive or negative) of triangle side lengths whereas atan2 keeps them in tact. Why is this important? Well, if we swing out $\frac{\pi}{4}$ along the unit circle in the anti-clockwise direction (with unit side lengths of the triangle formed) or diametrically by $-\frac{3\pi}{4}$ (with negative unit triangle side lengths), atan will give the same answer for both $\frac{y}{x}$ ratios — whoops. Here’s that subtle gotcha in Swift with a CoreGraphics import.

import CoreGraphics

atan(CGFloat(-1) / -1) == atan(CGFloat(1) / 1) // ⇒ true
atan(CGFloat(1) / 1) == .pi / 4 // ⇒ true

atan2 resolves this collision by separating out the lone $\frac{y}{x}$ CGFloat passed to atan into two arguments in $y$-first-then-$x$ order.

// Along the unit circle, anti-clockwise (positive radian direction).
atan2(CGFloat(1), 1) == .pi / 4  // ⇒ true
atan2(CGFloat(1), -1) == 3 * .pi / 4  // ⇒ true
atan2(CGFloat(0), -1) == .pi  // ⇒ true

// Along the unit circle, clockwise (negative radian direction).
atan2(CGFloat(-1), 1) == -.pi / 4  // ⇒ true
atan2(CGFloat(-1), -1) == -3 * .pi / 4  // ⇒ true

Moreover, TIL the phrasing around resolving collisions from integer multiples of $2\pi$ being added to any angle without changing the resulting $x$ or $y$: “restricting to principal values.”

atan is restricted to $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ principal values — to account for the domain spanning from $\left(\texttt{-CGFloat.infinity}, \texttt{.infinity}\right)$ — and atan2 to the range $\left(-\pi, \pi\right]$.

Modifying the pairwise operator with a duplicated start

11 Feb 2021 Bas van Kuijck PR’d Publisher.pairwise() (and .nwise(_:)) to CombineExt back in August and the operator came up in iOS Folks’ #reactive channel the other day. Jon Shier asked:

I need to compare changes to values within a sequence, they’re non-optional already, so I need a way to see the previous value and the current value. I could probably figure that part out, but what about the first pair? I can’t wait until I get two values and I’d rather not introduce optionals, but what if I duplicated the first value that came down the stream but otherwise always had the previous and current values?

Unfortunately, pairwise — which is an overlay on nwise(2) — will only send values downstream after two are received from its upstream. So, it doesn’t meet the “I can’t wait until I get two values” requirement.

And further, the “rather not introduce optionals” mention makes things trickier. Let’s take a look. An initial approach we could take is shareing upstream, spitting it off into two —  one left as is and another that’s first’d — and then connecting the split sequences with a flatMap that duplicates the first value and then finally pairwiseing the result (…that probably made zero sense in prose, here’s a sketch hah).

(Gist permalink.)

The repeat (1, 1) surprised me — I had assumed shareing upstream would ensure that the resubscribe in the flatMap would carry on with 2. I scratched my head and dug further into this bit.

(Gist permalink.)

The second subscription to upstream in the flatMap seems to synchronously win out over the lingering 2 from the first subscription (notice it comes in at the bottom of the logs, yet never makes it to the Post-share print operator). We can further suss out this race condition by delaying the first value event and then noticing the second subscription missed its chance entirely.

(Gist permalink.)

Stepping back, there miiight be a way to make a share based approach without race conditions like this while also accounting for upstream’s temperature (please reach out, if you know how (!)), but at this point, I decided to ease the “rather not introduce optionals” requirement and use a scan-based approach to work around these concerns.

(Gist permalink.)

The core of the implementation is at (1) — to kick off the scan, we coalesce the initial (nil, nil) to (next, next) for the first upstream value. From then on, we pair à la pairwise since subsequent calls to optionalZip will have a non-nil return value. It’s a bit unfortunate that the local, free-function optionalZip couldn’t simply be named zip, since that would collide with Publisher.zip in the implementation. Adam mentioned he runs into this often with Swift.print and Publisher.print, too. Wonder if there’s any reason Swift can’t have an inverse to the @_disfavoredOverload annotation — maybe called @_preferredOverload — to nudge the compiler here? We could prefix with the current module’s name in most cases, but I was working within a Playground (and I’m guessing they have generated module names that are out of reach at compile time).

AnyCancellable.store(in:) thread safety

31 Jan 2021 Thready safety has been a weak point for me (my university’s OS class also being taught in pre-1.x Rust didn’t help much, either hah); but, I’m slowly working on it.

Kyle Bashour’s reply to Curtis Herbert’s (Twitter) thread on the thread safety of AnyCancellable.store(in:) (or analogously, for the RangeReplaceableCollection overload) reminded me of a Combine gotcha. Swift’s Standard Library data structures aren’t thread-safe out of the box — which, in turn means we need to be extra careful when storing cancellation tokens across threads. Let’s tee up an example to see why.

(Gist permalink.)

If fetchCount is called across multiple threads, .store(in:) will concurrently modify cancellables, possibly leading to race conditions. There’s even a related issue about this over on OpenCombine’s repository. So, we’ll need to lock around the store call and while we could do the usual NSLocking.lock and .unlock dance, I looked around to see if we could do better. And I found a small helper over in TCA and in RxSwift.

extension NSRecursiveLock {
  @inlinable @discardableResult
  func sync<Value>(_ work: () -> Value) -> Value {
    lock()
    defer { unlock() }
    return work()
  }
}

We can then lean on this extension in our earlier example.

(Gist permalink.)

Prior art for this helper seems to be DispatchQueue’s sync(execute:) method. It might be tempting to further roll this logic up into an @Atomic property wrapper, yet it unfortunately won’t help when fencing off collection types — like Set in our case — because each thread would operate on its own copy of the data structure. Donny Wals walks through this in detail in a post on the topic.

Mapping over the range and pattern matching operators

30 Jan 2021 Two tricks for the operator and point-free-leaning crowd:

1. To quickly form ranges from a sequence of indices, you can use zip(indices, indices.dropFirst()).map(..<) (or subbing in the closed range operator — the one-sided variants are ambiguous in the point-free style)¹.

    let odds = [1, 3, 5, 7]
   
    zip(odds, odds.dropFirst()).map(..<) // ⇒ [(1..<3), (3..<5), (5..<7)]
   

2. And tangentially, to test if parallel sequences of ranges and values match against one another.

    // (…continuing from above.)
   	
    let odds = [1, 3, 5, 7]
    let oddRanges = zip(odds, odds.dropFirst()).map(..<)
   	
    let evens = [2, 4, 6]
    zip(oddRanges, evens).map(~=) // ⇒ [true, true, true]
   

Constant bindings as placeholders

27 Jan 2021 When building layouts in SwiftUI, I’ll often sketch out the views — ignoring data flow — and then turn my attention towards state management. However, since many view initializers require bindings (e.g. TextField.init or Toggle.init), that puts things in an awkward spot.

What do I slot in if I haven’t determined whether to back the view with @State, @ObservedObject, another @Binding, TCA-backed state, or the like?

Is there a placeholder I can use in the same way fatalError appeases the compiler while I think through an implementation?¹

Brandon and Stephen showed a technique early in episode #131 (timestamped).

For now, we’ll use a constant binding because we don’t have anywhere to send the user’s changes, but we will get to that soon.

Aha! That’s a solid trick — here’s a Toggle example with its binding fixed to false.

import SwiftUI

struct SampleView: View {
  var body: some View {
    Toggle("A toggle", isOn: .constant(false))
  }
}

Publisher.zip completions

23 Jan 2021 Zipping — in general — is a pairwise affair. Optional’s zip is non-nil if both arguments are. Similarly for Result’s zip along the .success case. Swift.zip pairs until it runs off the shorter of the sequence arguments. Parsers.Take2 (another name for zipped parsing) succeeds if both parsers involved do.

While Publisher.zip and its higher-arity overloads follow suit for value events, there’s a subtle gotcha for .finished events (failures are immediately passed downstream).

A zipped publisher can complete even if all of its inner publishers don’t.

(Gist permalink.)

This checks out after a pause — since second completes after the first (1, 2) pair comes through, there’s no chance it’ll pair with any future value events from first. Hence the completion. So, even though zipping is usually synonymous with “pairing” in my head, I’ll need to remember that doesn’t necessarily extend to completion events.

Buffered and batched subscriptions in Combine

23 Jan 2021

Updates:

1/23/20:

PR’d Collection.batchedSubscribe(by:) to CombineExt.

Yariv asked a great question in iOS Folks’ #reactive channel the other day:

I’m creating an array of URLSession.DataTaskPublishers — is there a way to perform them fifty at a time?

…I think Publisher.collect(50) will cache the responses and return them in batches, but they’ll be subscribed to all at once.

They’re spot on about Publisher.collect(_:)’s behavior — if we flatMap a sequence of publishers and then collect, the operator will subscribe to all of the upstream publishers and then emit their outputs in batches. Here’s a condensed example.

(Gist permalink.)

Ideally, we’d subscribe to upstream publishers and output in batches, bailing out if any publisher fails along the way. Adam quickly chimed in with a solution and Nate, Shai, and I worked on another that also guarantees ordering within each batch.

…throw a Publisher.buffer(size:prefetch:whenFull:) before the flatMap and then use its optional maxPublishers argument to limit the number of concurrent requests.

— Adam

Translating this into a constrained extension on Sequence:

(Gist permalink.)

There’s three bits to note. First, flatMap will subscribe to (up to) size many publishers and let their outputs come in as is, not guaranteeing ordering within each batch. We can randomly tweak the delay in the earlier example to show this:

(Gist permalink.)

Second is flatMap’s maxPublishers argument allows for size publishers to be in-flight at once. That is, there will always be at most size subscribed publishers from upstream until they all complete or any one fails. This is slightly different than subscribing to size publishers, waiting for that batch to entirely complete (or fail), and then subscribing to the next size publishers (strictly batched subscribing and outputting). I’ll refer to Adam’s approach as “buffered subscribing, batched outputting.”

And the third note is about the buffer call. Adam mentioned,

buffer may or may not be necessary depending on how upstream handles demand, since one way of handling backpressure is dropping upstream values.

Thankfully Publishers.Sequence — returned from the line above the buffer call — handles backpressure without dropping unrequested values, so we don’t need explicit buffering. Which begs the question? When would value dropping happen?

Turns out Tony Parker noted one instance over in the Swift Forums.

…the behavior you’re seeing is about the PassthroughSubject and not flatMap. PassthroughSubject will drop values if the downstream has not made any demand for them.

Aha! Let’s whip up a quick example to show this.

(Gist permalink.)

The 2 gets dropped since subscriber’s demand was .none when it was sent — the OpenCombine folks also picked up on this detail in their implementation. That tangent aside, and in short, Adam’s approach to buffered subscribing, batched outputting is as follows.

(Gist permalink.)

⬦

Now, for strictly batched subscribing and outputting. Rephrased, subscribing to (up to) limit publishers, waiting until they all complete (or fail), outputting the batch in their originating order, and repeating until all publishers are exhausted. This was where Shai and Nate lent a hand. We’ll need to pin batchedSubscribe(by:) below to Collection, since we’ll lean on its count property to calculate batch offsets.

(Gist permalink.)

There’s…a lot going on here — let’s start at indexBreaks.

indexBreaks plucks out every limit index within startIndex..<endIndex, which are then mapped into Ranges on line 16 by traversing indexBreaks pairwise on 15. Then, we convert to a publisher, tee up the failure type, flatMap one batch at a time onto the CombineExt.Collection.zip’d subrange of self, and finally erase out to an AnyPublisher (try saying this ten times fast hah).

(We don’t need a buffer call before line 19 since setFailureType directly subscribes downstream to its upstream, which in this case is Publishers.Sequence and it doesn’t drop unrequested values.)

Using batchedSubscribe(by:) in the randomly-delayed example now keeps in-batch ordering.

(Gist permalink.)

⬦

Phew! It’s wicked that Yariv’s question shook out 600+ words of detail. If you end up using batch subscriptions for a client-server synchronization scenario, keep in mind that you might want to materialize to avoid any one request from bottoming out the entire sync attempt. I learned this the hard way back at Peloton when pairing this approach with a retry operator that accidentally ended up…self-DDoSing our API when some users’ historical workouts kept 500’ing (for reasons we couldn’t quickly triage during the incident). But, I’ll save learnings from that story for another entry.

little self, Big Self

18 Jan 2021 Yesterday I learned — let’s pretend “YIL” is a thing — Swift’s postfix self (i.e. .self) can be used after any expression (not just types). It’s a lesser-known arcanum in the language.

1.self // ⇒ evaluates to 1.
"ayy lmao".self // ⇒ evaluates to "ayy lmao".
"ayy lmao".self.count // ⇒ evaluates to 8.
"ayy lmao".self.count.self % 2 // ⇒ evaluates to 0.

Unlike TypeName.self metatype expressions, SomeExpression.self postfix self expressions evaluate to the value of the expression. Which adds color to the decision behind \.self as the identity key path — it’s a sort of postfix self as a key path. QuinceyMorris noted in a Swift Forum’s thread that this precedent comes from the Objective-C days,

For historical, Objective-C* reasons, you can add .self to pretty much any expression and the resulting value is that same expression’s value.

[…]

*In Objective-C, [key-value coding (KVC)] always requires an object and a non-empty key-path to access a value. To reference the object itself, you don’t have a key-path, so NSObject defined a self method, which works as key-path “self” in KVC. It works like this in Swift, too:

let myself = self[keyPath: \.self]

⬦

To make things doubly esoteric, I might’ve had too much cold brew one morning when I realized Self.self is a valid expression and can be used to back Identifiable conformances for one-off alerts or sheets in SwiftUI.

(Gist permalink.)

Self.self allows id to follow suit with the type’s name, if it’s ever refactored down the line.

⬦

For more on Swift’s other selfs, Jesse Squires has you covered in a recent blog post.

Simultaneously mapping over publisher values and errors

31 Dec 2020 Dalton nerd sniped me earlier today when he asked:

Combine question: I’d love a “map”-like operator that is failable — like tryMap — but where I end up with a strongly-typed Error. I’m picturing something akin to,

func mapResult<NewOutput, NewFailure>(_ transform: @escaping (Result<Output, Failure>) -> Result<NewOutput, NewFailure>) -> AnyPublisher<NewOutput, NewFailure>.

Does this exist in the framework?

It doesn’t, yet Result and Result.publisher make this wicked fun to pull off.

The transform argument is also a specialized form of Either.bimap hiding in plain sight.

Redirecting Publisher errors

19 Dec 2020 Adam Sharp posted a snippet in iOS Folks today that I wanted to highlight (with a couple of light CombineExt-imported edits).

This is a form of materialization that feels more at home in Combine. It tucks away the awkward materialize-share-errors dance and instead focuses on funneling a publisher’s errors directly to a @Published property.

It’s tempting to use Publisher.share at (1) — and Adam avoided it for good reason. share implicitly autoconnects, which could accidentally trigger a subscription too early at the assign call at (2). Instead, he wired up the error-focused publisher to a multicasted PassthroughSubject (which returns a ConnectablePublisher) and then makes sure both subscriptions are properly teed up by autoconnecting the returned publisher at (3).

Mapping with parsers

24 Nov 2020 The first exercise from Point-Free episode #126 felt familiar. It asks the viewer to extend Parser with a placeholder-named method, f, which accepts another parser from Output to a possibly different output, NewOutput, to then return a parser of type Parser<Input, NewOutput>.

Behind the nominal garnish, a Parser is a function from (inout Input) -> Output?. So, it checks out that we can tee up parsers as long as their outputs and inputs match — the tricky bit is rolling back any modifications to the Input argument, if the first parsing succeeds and the second fails:

extension Parser {
  func f<NewOutput>(
    _ parser: Parser<Output, NewOutput>
  ) -> Parser<Input, NewOutput> {
    .init { input in
      let original = input

      guard var firstOutput = self.run(&input) else { return nil }
      guard let secondOutput = parser.run(&firstOutput) else {
        input = original
        return nil
      }

      return secondOutput
    }
  }
}

We’re lifting a Parser<Input, Output> to a Parser<Input, NewOutput> with the help of a Parser<Output, NewOutput>. Or in prose, we’re mapping a parser with a parser‽

Sans the inout rollback dance, this situation is almost the same as CasePath.appending(path:) (.. in operator form). CasePath.extract’s (Root) -> Value? shape is Parser.run’s immutable analog. Which hints that we can lift a case path into a parser.

import CasePaths

extension Parser {
  init(_ path: CasePath<Input, Output>) {
    self.init { path.extract(from: $0) }
  }
}

Parsing and case paths (prisms) appear linked in ways I have a feeling Jasdev-a-couple-of-years-from-now will better grok slash be too-hyped about and to get there, I’ll probably need to watch Fraser Tweedale’s ‌Unified Parsing and Printing with Prisms a few more times. It’s exciting that their approach seems to ease the partial isomorphism requirement proposed section 3.1 of the original Invertible Syntax Descriptions paper (e.g. a request parser doesn’t necessarily need to make a round trip when printing back the result of its parsing phase — a scenario that comes mind is an incoming request with unparsed query parameters getting nixed on the printing phase of the round trip).

combineLatest’ing an empty collection

21 Nov 2020 Palle asked a thoughtful question in an issue on the CombineExt repository the other day:

When calling Collection.combineLatest on an empty collection of publishers, an empty publisher is returned that completes immediately.

Instead, wouldn’t it make sense to publish just an empty array instead (Just([Output]()))?

And they have a point. Even though CombineExt and RxJS (links to each’s handling) return an empty sequence, RxSwift forwards the result selector applied to an empty array before completing and ReactiveSwift even allows for an emptySentinel to be specified in this case.

I can understand both camps.

• One could argue that combineLatest should only emit when any one if its inner observables does and if there are none then it’s a no-go for value events (i.e. return an empty sequence).
• One could also argue that by not emitting a value event, this behavior truncates operator chains that might back UIs dependent on non-terminal events. Think fetchArrayOfFriendIDs.flatMapLatest { ids in ids.map(publisherOfFriendDetails).combineLatest() }.bind(…)… — the bindee (?) would never hear back if we completed immediately in the empty ids case.

Here’s a quick workaround to land in the second camp while using CombineExt and then I wanted to note some theory that supports the position.

import CombineExt

[Just<Int>]() // (1) `Just<Int>` for sake of example, any `Publisher` will do.
  .combineLatest()
  .replaceEmpty(with: []) // (2) Forward a `[]` value event.

Now for the — cracks knuckles — theory.

To derive a non-empty publisher value of [Just<Int>]().combineLatest(), we’ll take the approach the Point-Free duo did back in episode #4 (timestamped) when they asked what a function product: ([Int]) -> Int, which multiplies the supplied integers together, should return when called with an empty array.

Translating their approach means figuring out how combineLatest should distribute across array concatenation,

[Just(1)]
  .combineLatest()
  .combineLatest(
    [Just<Int>]()
      .combineLatest()
  ) // Yields a `Publisher<([Int], [Int])>`.

should ≈

([Just(1)] + [Just<Int>]()).combineLatest() // Yields a `Publisher<[Int]>`, hence the `≈`.

The righthand side of the equals sign evaluates to a publisher that emits a sole [1], which forces our hand on the left side. [Just<Int>]().combineLatest() needs to return at least one value event to avoid cutting off the [Just(1)].combineLatest() before it from emitting.

If [Just<Int>]().combineLatest() emits a sole [] then the first expression will emit a ([1], []) — which is why we can only use approximate equality because there’s an isomorphism between [1] and ([1], []) in the same way there’s one between 1 and (1, ()) in tupled form.

All of this is to sketch out that if we view combineLatest¹ as a monoidal operator, then a publisher that emits a single [Output]() (i.e. Just([Output]())) acts as the unit and in turn, the result of the empty product under the operation.

From parsing operators to methods

19 Nov 2020 Updates:

11/19/20:

Stephen and I chatted about the reasoning behind the <%> symbol choice (instead of overloading the <*> operator like in the original invertible syntax descriptions paper).

It comes down to the authors using <*> in both a left- and right-associative manner, which isn’t possible in Swift and why swift-prelude split out its apply operators. Having a single operator with both associativities allows for the same expression to be used in printing and parsing (snippet from section 3.2).

A sign of personal growth I’ve used while learning functional programming over the years is noticing when I grok types — in this case, custom operators — that previously felt out of reach. And recently, Point-Free’s older parsing operators: <%>, <%, %>, and <|> clicked after the duo rewrote them as methods in episodes #120 and 123.

Let’s step through each:

<%>

<%>’s new name is Parser.take(_:). The shape hints at its meaning by having both less-than and greater-than signs indicating that the outputs of both operands are paired (further suggesting how <% and %> behave).

parserOfA <%> parserOfB returns a Parser<Input, (A, B)>.

Brandon and Stephen probably chose the percentage symbol since the operator used in the original paper on invertible syntax descriptions is <*>, which is often reserved for applicative sequential application.

<%

As you probably guessed, <% zips two parsers and discards the result of the righthand one. Or as methods, these two Parser.skip(_:) overloads (the latter is used to skip over the first parser in a zipped chain).

%>

Conversely, %> discards the left and keeps the righthand result. What’s wicked is that the combinator methods can express this without a new name and instead as an overload on take constrained to Parser.Output == Void.

extension Parser where Output == Void {
  func take<A>(_ p: Parser<Input, A>) -> Parser<Input, A> {
    zip(self, p).map { _, a in a }
  }
}

<|>

Last up is the cousin of the previous three, the analog to Parser.oneOf(_:).

Akin to how Boolean ORs (||) short-circuit once a true value is evaluated, the <|> shape signals that the combinator will run each operand in order and stop when one parses successfully.

The operator both mirrors the original form in the previously-linked paper and follows suit with the Alternative typeclass requirement¹ from Haskell’s Prelude.

Hopefully this note can serve as a reference for folks reading through the router behind pointfree.co until it’s updated with the method forms of these parser combinators.

Empty reducers and the monoidal unit

08 Sep 2020 Most writing about monoids starts by listing out the axioms (or in programming, the protocol or type class requirements) before diving into examples. And as Jeremy Kun notes, “[this is not only confusing, but boring (!)] to an untrained student. They don’t have the prerequisite intuition for why definitions are needed, and they’re left mindlessly following along at best.”

The Point-Free duo does a wonderful job at avoiding this — episodes start with and cover examples until a common shape is noticed and then chip away specializations until a more general form, and in turn, the axioms shake out. Rephrased, making an axiom earn its keep by pointing out problems that occur in its absence.

In episode #116, Brandon and Stephen did just that with the Reducer type’s monoidal unit. Instead of conforming Reducer to Monoid, they instead guided us into a situation — disabling logic on redacted views — where an inert reducer is needed to avoid state mutations and side effects. Or under their library’s name, Reducer.empty.

They subtly dropped the need for this axiom roughly 16 minutes in and it felt worth the extra show note here.

For a longer treatment on the topic, here’s a timestamped link from one of Brandon’s older talks: “Composable Reducers and Effects Systems.”

Conditional gestures in SwiftUI

15 Aug 2020 Conditionally enabling a gesture in SwiftUI wasn’t as intuitive for me compared to other modifiers. Showing or hiding a view is an .opacity(someCondition ? 1 : 0) (or if-else in a ViewBuilder or .hidden()) away. But for gestures? It felt off to have to .gesture(someCondition ? DragGesture().onChanged { /* … */ }.onEnded { /* … */ } : DragGesture()), where the first branch returns a live gesture and the second, an inert one. The types returned from the ternary need to line up — there’s an AnyGesture eraser in the framework that usually helps in these situations, yet it still begs the question of which instance to erase in the disabled case.

A search online for “SwiftUI disable gesture” tops out with Paul Hudson’s post, “Disabling user interactivity with allowsHitTesting(_:)” and while that modifier works in some situations, it was too coarse for the one I was in. I needed to disable a drag gesture and keep a tap gesture on the same view in tact and allowsHitTesting wholesale disables both.

Poking around the Gesture protocol’s listed conformances had the answer I was looking for — Optional conditionally conforms to Gesture!

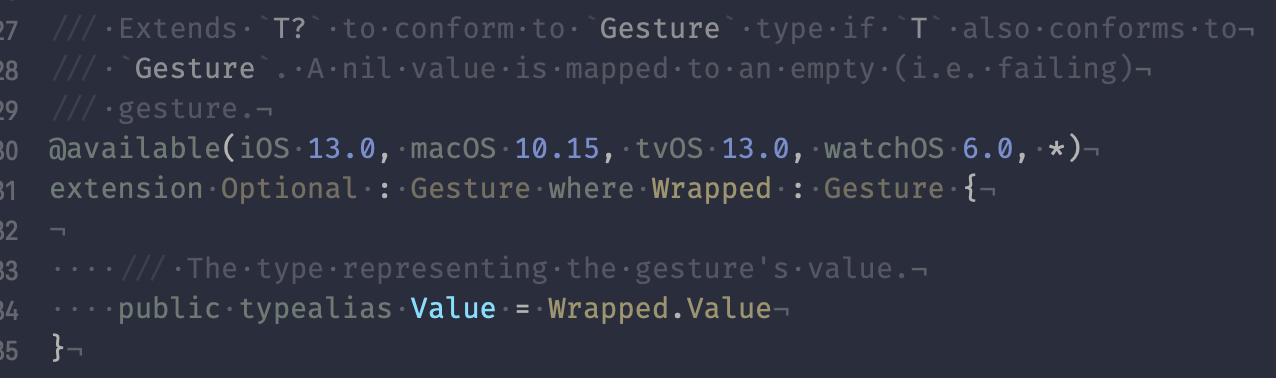
And Harlan Haskins helped me tidy the above ternary to .gesture(someCondition ? DragGesture().onChanged { /* … */ }.onEnded { /* … */ } : nil). What’s wicked here is the gesture is of type _EndedGesture<_ChangedGesture<DragGesture>> and Swift is able to promote the nil to an optionally-wrapped version without any added annotations.

Swimming out past intuition

26 Jul 2020 After a recent note on Binding[dynamicMember:], I’ve jokingly started a Twitter thread with the type’s affordances — à la Rob Rix’s “it type checks, but what does it mean?”

So far I’ve got Binding.zip and .flatMap (or alternatively, join paired with the dynamic member subscript).

(Gist permalink.)

Type checking drove the implementations since I don’t grok them yet. What does it mean to flatMap on Bindings? Is that something we’d even want to do?

The compiler signaled the “reachability” of these functions, even if my understanding wasn’t there. And this is why proof assistants like Lean and community efforts behind them (the Xena project) excite me. If mathematics can be formalized to a point where assistants can guide our work in the same way a compiler does for engineering, we can swim past our present intuitions.

It’ll take a while for our collective knowledge to catch up to a lengthened line of sight, but we also needed telescopes before we could physically explore space.

Why folks use <> for same-type composition

19 Jul 2020 A wondering I had back when I started studying FP in earnest was why folks used <> for same-type composition instead of the more general >>> operator (which stitches (A) -> Bs with (B) -> Cs).

And yesterday while re-watching Brandon Williams’ “Monoids, predicates and sorting functions” talk, I found a likely answer (timestamped link).

Functions in the form (A) -> A — endomorphisms — come with a semigroup (and monoidal) structure and the diamond operator is a nod to that. The operator is subtly interchangeable with >>> because Endo’s¹ conformance leans on function composition under the hood.

(Gist permalink.)

Pausing with Binding’s dynamic member subscript

19 Jul 2020 Roughly thirteen minutes into Point-Free episode #108 (timestamped), Stephen and Brandon showed how SwiftUI’s Binding type secretly has an implementation of map under the guise of its dynamic member subscript.

I didn’t fully realize the gravity of that statement until, well, a week later.

Binding is the first real-world functor I’ve used with two components — hidden by way of its .init(get:set:) initializer — of different variances. Value is in the covariant position on the getter and in the contravariant position on the setter. The only other two-component functors I’ve used — Either and tuples — are plain old bifunctors¹. And to make it even more opaque, the dynamic member subscript only accepts one argument, a WritableKeyPath<Value, Subject>, that can somehow handle the two variances.

Below is me pausing with and unpacking how this works.

First, let’s imagine implementing Binding.map without a WritableKeypath for a closer look.

(Gist permalink.)

In implementing (1), we have access to self.wrappedValue and need to conjure a Subject instance. Which means that Binding.map needs to accept a (Value) -> Subject transformation. Check.

(Gist permalink.)

Onto (2).

We need to implement (Subject) -> Void again with only a Value instance in hand. That is, a way to mutate our wrapped value with a Subject instance — shaking out the second parameter: (inout Value, Subject) -> Void.

(Gist permalink.)

Now it’s more explicit that mapping a Binding<Value> to a Binding<Subject>, requires two transformations. One with Subject in the covariant position (get) and the other in the contravariant (set).

Which then raises the question, how does Apple pull this off with only a WritableKeyPath<Value, Subject>?

Turns out the Writable* bit is important.

Binding.map’s get parameter can be satisfied by the fact that any KeyPath from Value to Subject is equivalent to a (Value) -> Subject function (with the help of SE-0249).

How about set?

Can we convert a WritableKeyPath<Value, Subject> to an (inout Value, Subject) -> Void function?

…we can! Let’s call the conversion setterFromKeyPath:

(Gist permalink.)

This conversion is how WritableKeyPath packs the get-set punch needed to call Binding[dynamicMember:] an implementation of map on the type.

A whole lot of detail packed into those first thirteen minutes of the episode, eh?

Stress testing variadic zip

23 May 2020 Yesterday, Daniel Williams and I messaged through a crasher he ran into when using CombineExt.Collection.zip (similarly with .Collection.combineLatest).

For the uninitiated, Combine ships with zip (and combineLatest) overloads up to arity four in the Publisher namespace.

• .zip(_:_:_:)
• .combineLatest(_:_:_:)

But, if you want to zip arbitrarily many publishers, you’re kind of stuck and as more Combine code gets written, folks are quickly realizing this. That’s why we’ve been heads down filling in gaps with an extensions package to sit next to Combine proper.

Daniel was attempting to first ping https://hacker-news.firebaseio.com/v0/topstories.json for an array of Hacker News story IDs and then hydrate each by hitting the https://hacker-news.firebaseio.com/v0/item/:id.json endpoint. The former returns on the order of 500 entries and that turned out to be enough to push variadic zip beyond its limits.

We can reduce the scenario down with convenience publishers for a closer look.

(Gist permalink.)

(You might need to tweak count to trigger the crash.)

The stack trace is a head scratcher.

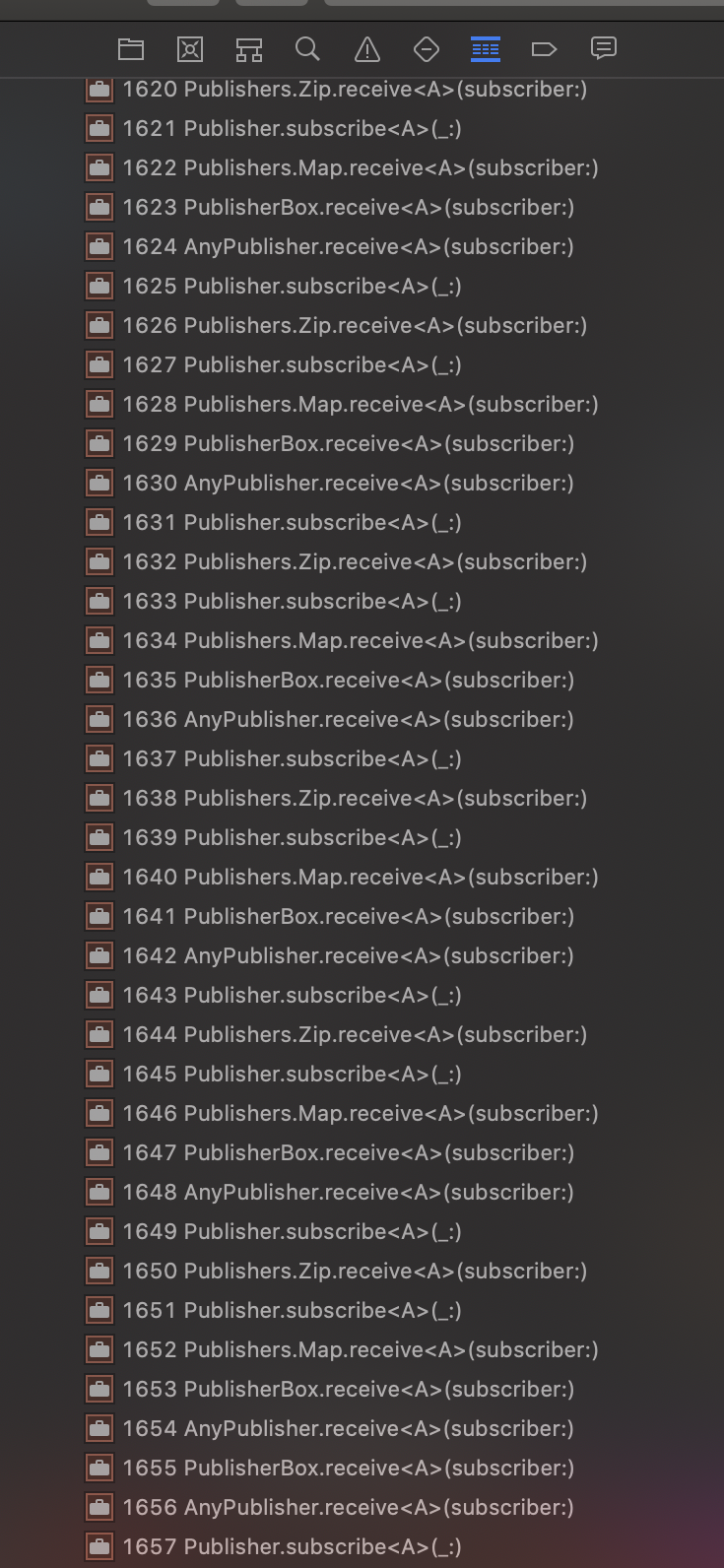
And the repeated Zip, Map, and PublisherBox frames hint at the issue.

CombineExt’s variadic zip and combineLatest are “composed” operators — they’re built up from existing Publisher methods instead of a more dedicated conformance. While this simplifies things and lets each implementation measure out to ~15 lines, it also introduces intermediate runtime overhead.

Let’s take a look at why (in shorter form, here’s the fuller implementation).

(Gist permalink.)

1. The only way to line up seed’s type with reduce’s accumulator is to erase — or, at least I tried without in hopes of preserving fusion and got type checked into a corner.
2. This and the following two lines are the source of the Zip, Map, and PublisherBox stack trace dance. As we approach thousands of publishers, we’re triply nesting for each.

Can we fix this?

Yep — by writing a specialized ZipCollectionType à la RxSwift’s! But with WWDC around the corner, it’s probably best to hang tight and see if the Combine team will address the gap.

Until then, and if you want to read more about variadic zipping, an older entry has your back.

Why “sink?”

25 Apr 2020 “Sink” is a word you’ll see all over reactive declarative programming, and Combine is no exception.

There’s Subscribers.Sink (the subscriber behind the two Publisher.sink overloads), CombineExt.Sink (albeit internally-scoped), and similarly in the framework’s predecessor, RxSwift.Sink.

The often-cited kitchen sink metaphor aside, the term’s etymology is a bit unclear. My guess would be it borrows from the corresponding graph theory term.

A local sink is a node of a directed graph with no exiting edges, also called a terminal.

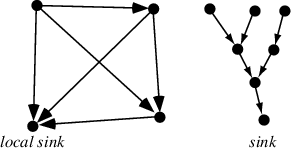
We can view a subscription graph as a directed graph between upstream publishers, through various operators, and down towards local sinks (which, in Combine’s language are Subscribers).

Profunctors generalize relations

25 Apr 2020 An aside before the note, Day One reminded me that I started studying category theory, in earnest, almost a year ago today.

Despite being a hobby, I’m pretty proud of how far I’ve come (I struggle with saying that aloud, since I’m the type to keep pushing forward and not really look around along the way).

I’m

• in a research group,
• followed along and typeset solutions for Programming with Categories,
• shot my shot and applied to Adjoint School and Causeway (got rejected from the former and the latter got cancelled—still, I tried),
• and am learning from and met incredibly kind folks like Jade, Sarah, and Jeremy.

Richard Guy put how I’ve felt as of late succinctly.

…and I love anybody who can [do mathematics] well, so I just like to hang on and try to copy them as best I can, even though I’m not really in their league.

(I’m not sure if anyone reads these entries hah (quite literally, I removed analytics on the site a few years ago). If so, pardon the moment to reflect.)

⬦

I was revisiting profunctors yesterday and Bartosz mentioned an intuition in lecture III.6.1 (timestamped) that made their motivation click.

You can think of a profunctor as [generalizing] a relation between objects.

Huh, okay. Let’s take a step back and recap what a relation is in plain ol’ set theory and follow the intuition.

A binary relation over two sets $X$ and $Y$ is a subset of their Cartesian product, $X \times Y$. That is, a set of ordered pairs indicating which $X$s are related to specific $Y$s.

And now to generalize.

First, let’s swap out the sets for categories $C$ and $D$.

$C \times D$. Okay, the product category. Since $C$ and $D$ are possibly distinct categories, we can’t directly consider morphisms between them. But, we can in their product category—morphisms between objects $(c, d)$ and $(c^\prime, d^\prime)$ are those in the form $(f, g)$ with $f: c \rightarrow c^\prime$ and $g: d \rightarrow d^\prime$. So, in a sense, the collection of relationships between $c$ and $d$ is $\textrm{Hom}((c, d), (c^\prime, d^\prime))$.

That hom-set is, well, a set (assuming we’re working with small categories)! What if we tried to create a functor from $C \times D \rightarrow \mathbf{Set}$ defined by $(c, d) \mapsto \ldots$

Wait. $c$ and $d$ come from different categories and hom-sets only work in a single category. I read around to reconcile this and stumbled upon heteromorphisms. “Morphisms” between two objects from different categories that use a bridging functor to then construct a hom-set. I got lost trying to read further, and with warning from slide 3/41 of David Ellerman’s presentation on the topic.

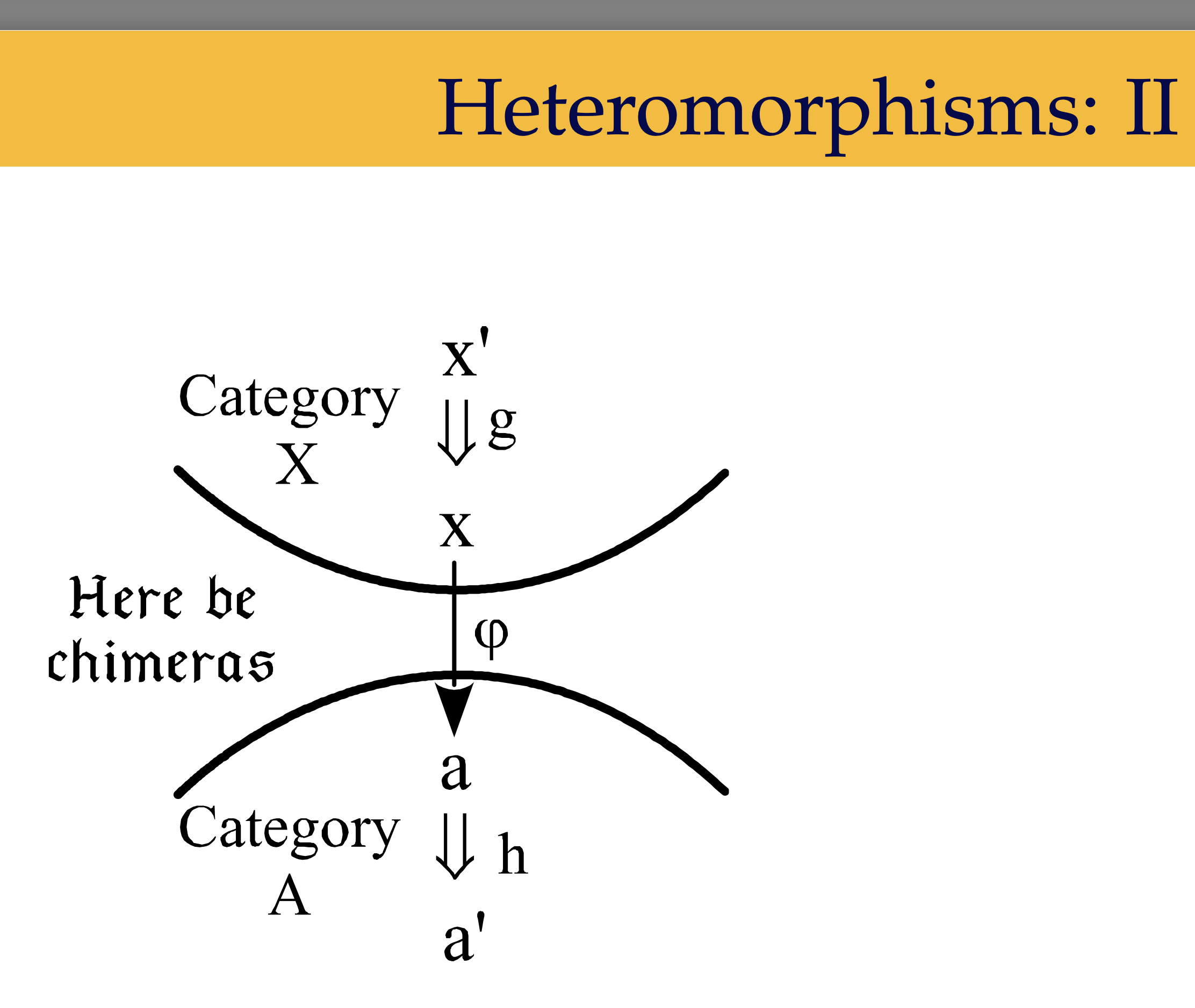
So, let’s assume $C = D$ and carry on (I’ll understand that presentation someday).

Okay, let’s map $c, d$ (both objects in $C$) to $\textrm{Hom}(c, d)$. And for morphisms, we need to map some $(f, g)$ for $f: c \rightarrow c^\prime$ and $g: d \rightarrow d^\prime$ to a function between $\textrm{Hom}(c, d)$ and $\textrm{Hom}(c^\prime, d^\prime)$. Let’s pluck out a morphism, say $h$ from $\textrm{Hom}(c, d)$.

We have $f, g, h$ in hand and need to construct a morphism from $c^\prime$ to $d^\prime$. There’s…no way to do this. None of our morphisms map from $c^\prime$.

That’s where the contravariance in the profunctor construction comes from when folks write $C^{\textrm{op}} \times C \rightarrow \mathbf{Set}$ (or, in the general case $C^{\textrm{op}} \times D \rightarrow \mathbf{Set}$). Taking the dual in the first component of the product category flips $f$ and now lets us get from $c^\prime$ to $d^\prime$ by way of $g \circ h \circ f$.

It’s okay if you need to walk around the park with that composition before it makes sense. I certainly needed to and it demystified the rogue dimap’s I’d see in Preludes.

But, let’s take stock on how this generalizes relations. In the same-category setting, we’re constructing a functor that maps two objects to the ways in which they’re related, their hom-sets. Since it’s a functor, we also need to consider mapping morphisms across the functor into functions between hom-sets and dimap (link to Haskell’s Prelude) does just that.

⇒ “Profunctors as relations”

⇒ “Understanding profunctors”

All metric spaces are Lawvere metric spaces

18 Apr 2020 I’m definitely the rookie in my research group, so the notebook will be a bit math-heavy as I try to catch up.

To start, here’s an entry on a topic—amongst many—Jade walked us through during our first meeting, Lawvere metric spaces.

nLab’s definiton is a bit impenetrable. At a glance, it seems like tacking on Lawvere’s name, to an already general concept, means added axioms.

It’s…surprisingly the opposite.

All metric spaces are Lawvere metric spaces—that is, we lift some of the constraints on plain ol’ metrics.

Recapping, a metric space is a set $X$ equipped with a distance function $d: X \times X \rightarrow [0, \infty)$ under the following coherences:

Assuming $x, y, z \in X$,

• $d(x, y) = 0 \iff x = y$ (zero-distance coincides with equality).
• $d(x, y) = d(y, x)$ (symmetry).
• $d(x, y) + d(y, z) \geq d(x, z)$ (the triangle inequality).

And Lawvere relaxed a few bits. A Lawvere metric space has a distance function

• that respects the triangle inequality,
• whose codomain includes $\infty$ (which is helpful when we want a “disconnectedness” between points),
• and $d(x, x) = 0$ (points are zero-distance from themselves).

We’re dropping the symmetry requirement and allowing for possibly zero distances between distinct points.

The former lets us represent, e.g. in a distance as cost situation, non-symmetric costs. Borrowing from Baez, imagine the commute from $x$ to $y$ being cheaper than from $y$ to $x$.

The easing of zero-distance being necessary and sufficient for equality to only one side of the implication adds the ability to reach points “for free” (continuing with the transportation theme).

I need to read up on more applications this freedom affords us. In the meantime, here’s some links I’ve come across:

• Jeremy Kun’s metric spaces primer.
• Lecture 31’s notes from MIT’s ’19 ACT course.
• Section 2.3.3 of Seven Sketches.

Easing AnyCancellable storage

10 Apr 2020 Quick note on a late-night PR I drafted for CombineExt. It tidies the repetitive AnyCancellable.store(in:) calls needed to hold onto cancellation tokens.

(Gist permalink.)

I’ve also added a Sequence variant.

And both are Element == AnyCancellable constrained to avoid crowding Set’s namespace.

Weak assignment in Combine

08 Apr 2020 Publisher.assign(to:on:) comes with a pretty big warning label,

The Subscribers.Assign instance created by this operator maintains a strong reference to object […]

and we need to read this label when piping publishers to @Published properties in ObservableObject conformances.

(Gist permalink.)

Of course, we could do the sink-weak-self-receiveValue dance. But, that’s a bit of ceremony.

(Gist permalink.)

My first instinct was to weak-ly overload assign and PR’d it to CombineExt, in case it’d help others, too. And with some distance and thoughtful feedback from both Shai and Adam, I decided to re-think that instinct.

There’s a few downsides to Publisher.weaklyAssign(to:on).

• It crowds an already packed Publisher namespace.
• In its current form, it doesn’t relay which argument is weakly captured. A clearer signature would be .assign(to:onWeak:) (and similarly, for an unowned variant).

Adam mentioned a couple of alternatives:

• “Promote” the weak keyword to a sort of function by way of a WeakBox type and assign onto it. I tried to make this work—learning more than I bargained for about dynamic member lookup along the way—and ran into a tradeoff dead end.
• Encode the weak capture semantics at the type level à la the Bindings package. Which, felt a bit out of scope for CombineExt, since it’s more of an operator collection.

So, I’m back to where I started and with a slightly modified overload. Gist’ing it below for the curious.

(Gist permalink.)

Now call sites can read—

(Gist permalink.)

Ah! Almost forgot. Writing tests for the operator had me reaching for Swift.isKnownUniquelyReferenced(_:)—“a [free-function] I haven’t heard [from] in a long time, a long time.”

There’s sliced bread, and then Result.publisher

07 Apr 2020 Another learning from Adam.

A situation I often find myself in is sketching an operator chain and exercising both the value and failure paths by swapping upstream with Just or Fail, respectively.

And it turns out that Apple added a Combine overlay to Result with the .publisher property that streamlines the two. That is, while all three of Just, Fail, and Result.Publisher have their uses, the latter might be easier to reach for in technical writing. Moreover, it’s a quick way to materialize a throwing function and pipe it downstream.

(Gist permalink.)

Or, as I’ll call it going forward—“the ol’ razzle dazzle.”

pic.twitter.com/o7EcZqNBlj

— Jasdev Singh (@jasdev) April 6, 2020

Postfix type erasure

25 Mar 2020 A belated entry on an operator I posted before…all of this (gestures wildly) started.

⬦

There’s nuance in determining whether or not to type erase a publisher—my next longer-form post will cover this—but when you need to, eraseToAnyPublisher()’s ergonomics aren’t great.

It requires 22 characters (including a dot for the method call and Void argument) to apply a rather one-character concept.

And I know operators are borderline #holy-war—still, if you’re open to them, I’ve borrowed prior art from Bow and Point-Free by using a ^ postfix operator.

It passes the three checks any operator should.

• Does the operator overload an existing one in Swift? Thankfully not (since bitwise XOR is infix).
• Does its shape convey its intent? To an extent! The caret hints at a sort of “lifting” and that’s what erasure is after all. Removing specific details, leaving behind a more general shape.
• Does it have prior art? Yep.
  • Bow defines one to ease higher-kinded type emulation.
  • Point-Free defined a prefix variant to lift key path expressions into function form before SE-0249 landed in Swift 5.2

The operator has tidied the Combine I’ve written so far. Here’s a gist with its definition.

Parity and arity

17 Mar 2020 Two tucked-away, somewhat-related terms I enjoy: parity and arity.

The former is the odd or even-ness of an integer.

The latter describes the number of arguments a function accepts.

Example usage of parity:

Today I learned about the Handshaking Lemma. It states that any finite undirected graph, will have an even number of vertices with an odd degree.

The proof rests on parity. Specifically, if you sum the degrees of every vertex in a graph, you’ll double count each edge. And that double counting implies the sum is even, and even parity is only maintained if there is an even—including zero—number of vertices with an odd degree.

Put arithmetically, a sum can only be even if its components contain an even number of odd terms.

Examples of arity:

• Swift’s tuple comparison operators topping out at arity six.
• Publisher.zip is only overloaded to arity three.
  • I PR’d a variadic overload to CombineCommunity/CombineExt yesterday and have a post walking through it in the works.

Contrasting isomorphisms, equivalencies, and adjunctions

01 Jan 2020 When I was first introduced to adjunctions, I reacted in the way Spivak anticipated during an applied category theory lecture (timestamped, transcribed below).

…and when people see this definition [of an adjunction], they think “well, that seems…fine. I’m glad you told me about…that.”

And it wasn’t until I stumbled upon a Catsters lecture from 2007 (!) where Eugenia Cheng clarified the intent behind the definition (and contrasted it to isomorphisms and equivalencies).

To start, assume we have two categories C and D with functors, F and G between them (F moving from C to D and G in the other direction).

There are a few possible scenarios we could find ourselves in.

• Taking the round trip—i.e. GF and FG—is equal to the identity functors on C and D (denoted with 1_C and 1_D below).
• The round trip is isomorphic to each identity functor.
• Or, the round trip lands us a morphism away from where we started.

Moving between the scenarios, there’s a sort of “relaxing” of strictness:

• The round trip is the identity functor.
• […] an isomorphism away from the identity functor.
• […] a hop away from identity functor.

Why optics?

15 Dec 2019 The better part of my weekend was spent reading Chris Penner’s incredibly well-written Optics by Example and attempting the exercises with BowOptics.

I’m early in my learning. Still, I wanted to note the motivation behind optics.

They seek to capture control flow, which, is usually baked into languages with for, while, if, guard, switch, and similar statements, as values.

In the same way that effect systems capture effects as values—decoupling them from execution—optics separate control flow when navigating data structures from the actions taken on them.

Sara Fransson put this well in their recent talk: Functional Lenses Through a Practical Lens.

■

Noticing that optics excite me much like FRP did back when I first learned about it.

And I haven’t even gotten to the category-theoretic backings yet.

(Attempts to contain excitement. Back to reading.)

TIL about Publishers.MergeMany.init

13 Dec 2019 A few weeks back, Jordan Morgan nerd sniped me¹ into writing a Combine analog to RxSwift’s ObservableType.merge(sources:)—an operator that can merge arbitrarily many observable sequences.

Here’s a rough, not-tested-in-production sketch (if you know a way to ease the eraseToAnyPublisher dance, let me know):

And in writing this entry, I decided to check and make sure I wasn’t missing something. After all, it’s odd (pun intended) that the merging operators on Publisher stop at arity seven.

Then, I noticed the Publishers.MergeMany return value on the first and, below the (hopefully temporary) “No overview available” note on its documentation, there’s a variadic initializer!

So, there you have it. TIL merging a sequence of publishers goes by the name of Publishers.MergeMany.init(_:).

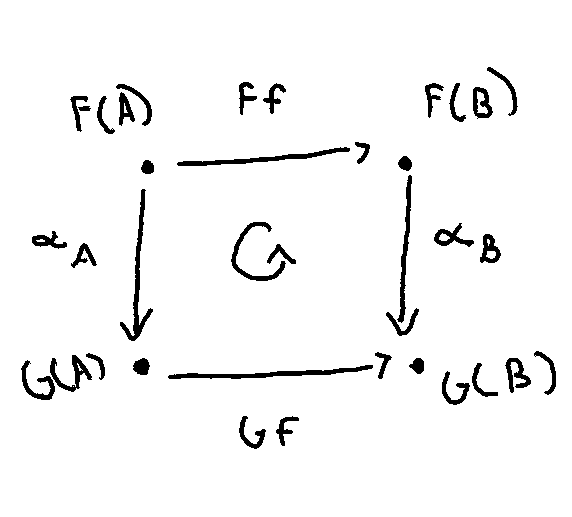
Naturality condition

01 Nov 2019 I’m currently working through Mio Alter’s post, “Yoneda, Currying, and Fusion” (his other piece on equivalence relations is equally stellar).

Early on, Mio mentions:

It turns out that being a natural transformation is hard: the commutative diagram that a natural transformation has to satisfy means that the components […] fit together in the right way.

Visually, the diagram formed by functors F and G between C and D and with natural transformation α must commute (signaled by the rounded arrow in the center).

I’m trying to get a sense for why this condition is “hard” to meet.

What’s helped is making the commutativity explicit by drawing the diagonals and seeing that they must be the equal. The four legs of the two triangles that cut the square must share a common diagonal.

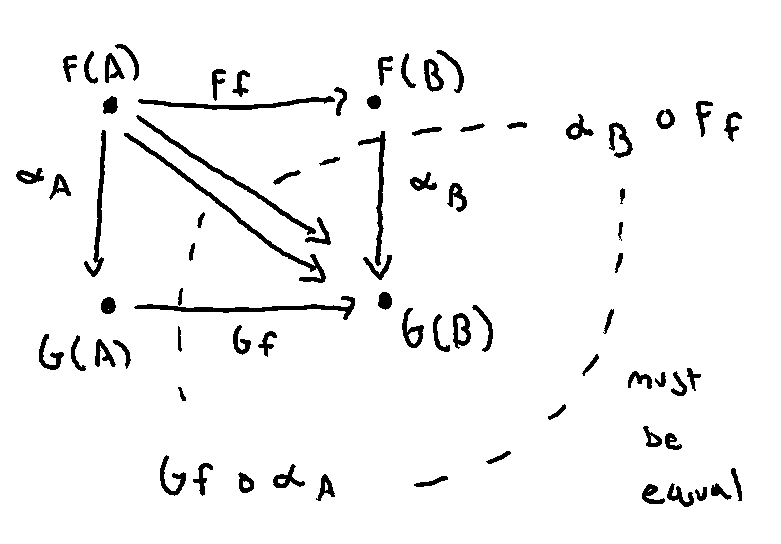
Maybe that’s why natural transformations are rare? There might be many morphisms between F(A) and G(A) and F(B) and G(B), but only a select few (or none) which cause their compositions to coincide.

For more on commutative diagrams, Tai-Danae Bradley has a post dedicated to the topic.

Why applicatives are monoidal

27 Oct 2019 “Applicative functors are […] lax monoidal functors with tensorial strength.”

I still don’t quite have the foundation to grok the “lax” and “tensorial strength” bits (I will, some day). Yet, seeing applicatives as monoidal always felt out of reach.

They’re often introduced with the pure and apply duo (sketched out below for Optional).

(An aside, it finally clicked that the choice of “applicative” is, because, well, it supports function application inside of the functor’s context.)

And then, coincidentally, I recently asked:

is there any special terminology around types that support a zip in the same way functors have a map and monads have a flatMap?

To which, Matthew Johnson let me in on the secret.

zip is an alternate way to formulate applicative

!!!.

That makes way more sense and sheds light on why Point-Free treated map, flatMap, and zip as their big three instead of introducing pure and apply.

I can only sort of see that apply implies monoidal-ness (pardon the formality) in that it reduces an Optional<(A) -> B> and Optional<A> into a single Optional<B>. However, the fact that they contained different shapes always made me wonder.

zip relays the ability to combine more readily. “Hand me an Optional<A> and an Optional<B> and I’ll give you an Optional<(A, B)>.”

Yesterday, I finally got around to defining apply in terms of zip to see the equivalence.

Funnily enough, Brandon pointed me to exercise 25.2 which asks exactly this.

In short,

• Functors allow for a map.
• Applicatives, a zip.
• Monads, a flatMap.

Type erasure and forgetful functors

24 Oct 2019 Type erasure and forgetful functors, at least in terms of intuition, feel very similar.

One removes detail (e.g. Publishers.Zip -> AnyPublisher) and the other strips structure, leaving the underlying set behind (a monoid or group being mapped onto its base set).

Wonder if there’s a way to visualize this by considering eraseToAnyPublisher as a sort of forgetful endofunctor into a subcategory of Swift (hand waving) that only contains AnyPublishers?

Co-, contra-, and invariance

20 Oct 2019 Folks often refer to the component of a function’s “polarity.” “The input is in the negative position.” “The output is positive.”

And that made me wonder, is there a, well, neutral polarity?

Maybe that’s when a component is in both a negative and positive position, canceling one another out.

Let’s see what happens.

A -> ….

A is in a negative position? Check. Let’s add it to the positive spot.

A -> A.

This is our old friend, Endo! At the bottom of the file, I noticed imap and asked some folks what the “i” stood for. Turns out it’s short for, “invariant,” which reads nicely in that both co- and contravariance net out to invariance.

Pairing functor type, variance(s), and *map name:

• Functor, covariant, map.
• Functor, contravariant, contramappullback.
• Bifunctor, covariant (and I’m guessing contra-, maybe both working in the same direction is what matters?), bimap.
• Invariant functor, invariant (co- and contravariant in the same component), imap.
• Profunctor, co- and contravariant along two components, dimap.

What makes natural transformations, natural?

19 Oct 2019 Learning category theory often involves patiently sitting with a concept until it—eventually—clicks and then considering it as a building block for the next¹.

Grokking natural transformations went that way for me.

I still remember the team lunch last spring where I couldn’t keep my excitement for the abstraction a secret and had to share with everyone (I’m a blast at parties).

After mentioning the often-cited example of a natural transformation in engineering, Collection.first (a transformation between the Collection and Optional functors), a teammate asked me the question heading this note:

What makes a natural transformation, natural?

I found an interpretation of the word.

Say we have some categories C and D and functors F and G between them, diagrammed below:

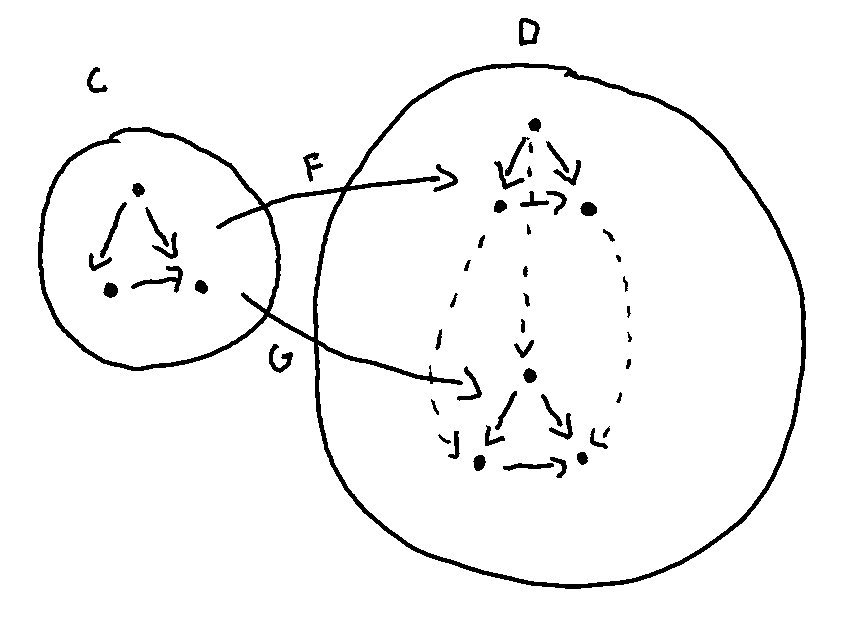
If we wanted to move from the image of F acting on C to the image of G, we have to find a way of moving between objects in the same category.

The question, rephrased, becomes what connects objects in a category? Well, morphisms!

Now, how do we pick them? Another condition on natural transformations is that the square formed by mapping two objects, A and B connected by a morphism f, across two functors F and G must commute.

Let’s call our choices of morphisms between F_A and G_A and F_B and G_B, α_A and α_B, respectively.

Even if f flips directions across F and G—i.e. they’re contravariant functors—our choice in α_A and α_B is fixed!

The definition, the choice of morphisms, seems to naturally follow from structure at hand. It doesn’t depend on arbitrary choices.

Tangentially, a definition shaking out from some structure reminds me of how the Curry–Howard correspondence causes certain functions to have a unique implementation. Brandon covered this topic in a past Brooklyn Swift presentation (timestamped).

For more resources on natural transformations:

• What is a Natural Transformation? Definition and Examples
• What is a Natural Transformation? Definition and Examples, Part 2
• Bartosz’s 1.9.1 lecture on the topic.

“Oh, the morphisms you’ll see!”

17 Oct 2019 There are many prefixes placed in front of the word “morphism”—here’s a glossary of the ones I’ve seen so far:

• Epimorphism
  • The categorical analog to surjectivity—the “epi” root connotes morphisms mapping “over” the entirety of the codomain. Bartosz covers this well in lecture 2.1 (timestamped) of Part I of his category theory course.
• Monomorphism
  • Injectivity’s analog and epimorphism’s dual (it blew my mind to realize injectivity and surjectivity, two properties I never thought twice about, are duals). “Mono” in that it generalizes one-to-one functions. Bartosz also mentions them in 2.1.
• Bimorphism
  • “A morphism that is both an epimorphism and a monomorphism is called a bimorphism.”
  • I don’t quite have the foundation needed to grok when a bimorphism isn’t an isomorphism—maybe because I spend most of my time working in Hask and Swift (Set, in disguise) and Wikipedia mentions “a category, such as Set, in which every bimorphism is an isomorphism is known as a balanced category.” On the other hand, and I need to read more into what “split” means in the following, “while every isomorphism is a bimorphism, a bimorphism is not necessarily an isomorphism. For example, in the category of commutative rings the inclusion Z ⇒ Q is a bimorphism that is not an isomorphism. However, any morphism that is both an epimorphism and a split monomorphism, or both a monomorphism and a split epimorphism, must be an isomorphism.”
• Isomorphism
  • Show up all over mathematics. A morphism that “admits a two-sided inverse, meaning that there is another morphism in [the] category [at hand] such that [their forward and backward compositions emit identity arrows on the domain and codomain, respectively].” “Iso” for equal in the sense that if an isomorphism exists, there is an sort of sameness to the two objects.
• Endomorphism
  • A morphism from an object onto itself that isn’t necessarily an identity arrow. “Endo” for “within” or “inner.” The prefix shed light on why the Point-Free folks named functions in the form (A) -> A, Endo<A>. Looking at that file now, I wonder what the “i” in imap stands for and I may or may not have gotten nerd sniped into checking if imap’s definition shakes out from Func.dimap when dealing with Func<A, A>s and Z == C == B (the B being imap’s generic parameter). Looks like it does?…a few messages later and Peter Tomaselli helped me out! The “i” stands for “invariant,” which reads nicely in that imap’s co- and contravariant parameters kind of cancel out to invariance.
• Automorphism
  • An isomorphic endomorphism. “Auto” for same or self.
• Homomorphism
  • The star of algebra, a structure-preserving mapping between two algebraic structures. i.e. a homomorphism f on some structure with a binary operation, say *, will preserve it across the mapping—f(a * b) = f(a) * f(b). I’ll cover the etymological relationship between “hom” and its appearances in category theory—hom-sets and hom-functors—that isn’t quite restricted to sets in the way algebra generally is in a future note.
• Homeomorphism
  • The one I’m least familiar with—in another life (or maybe later in this one), I want to dig into (algebraic) topology. Seems to be the topologist’s isomorphism (in the category Top).
• Catamorphism, Anamorphism, and Hylomorphism
  • I’ve only dealt with these three in the functional programming sense. Catamorphisms break down a larger structure into a reduced value (“cata” for “down”), anamorphisms build structure from a smaller set of values (“ana” for “up”), and hylomorphism is an ana- followed by a catamorphism (oddly, “hylo” stands for “matter” or “wood,” wat).
  • I ran into catamorphism the other day when trying to put a name on a function in the form ((Left) -> T) -> ((Right) -> T) -> (Either<Left, Right>) -> T. Turns out folks call this either, analysis, converge, or fold (the last of which was somewhat surprising to me in that the Foldable type class requires a monoidal instance, whereas this transformation doesn’t quite have the same requirement). This function is catamorphic in that it reduces an Either into a T.
  • zip is an example of an anamorphism that builds a Zip2Sequence from two Sequences and by extension, zipWith is a hylomorphism that zips and then reduces down to a summary value by a transformation.
  • Hylomorphisms and imap both seem to be compositions of dual transformations. Wonder if this pattern pops up elsewhere?

Getting an intuition around why we can call contramap a pullback

17 Oct 2019 Last October, Brandon and Stephen reintroduced contramap—covered in episode 14—as pullback.

(The analog for the Haskell peeps is Contravariant’s contramap requirement.)

However, the name contramap isn’t fantastic. In one way it’s nice because it is indeed the contravariant version of map. It has basically the same shape as map, it’s just that the arrow flips the other direction. Even so, the term may seem a little overly-jargony and may turn people off to the idea entirely, and that would be a real shame.

Luckily, there’s a concept in math that is far more general than the idea of contravariance, and in the case of functions is precisely contramap. And even better it has a great name. It’s called the pullback. Intuitively it expresses the idea of pulling a structure back along a function to another structure.

—“Some news about contramap”

I had trouble getting an intuition around why contramap’ing is a pullback, in the categorical sense and here’s why (mirroring a recent Twitter thread):

@pointfreeco—Hey y’all 👋🏽 I’m a tad confused when it comes to grounding the canonical pullback diagram with types and functions between them. (Pardon the rough sketch hah, I forgot my LaTeX and this was more fun. 😄) /1

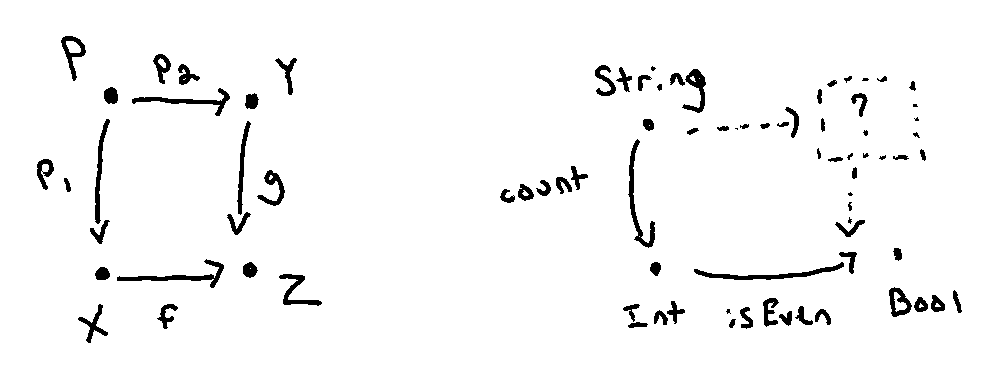
Pullbacks, generally, seem to give two morphisms and objects worth of freedom—f, g, X, and Y—whereas in code, we almost always seem to pullback along one [path across] the square. /2

Do y’all call this operation pullback because there isn’t a restriction preventing f from equaling g and X equaling Y (collapsing the square into a linear diagram)? /3

Yesterday, Eureka Zhu cleared up my confusion on why we don’t take the upper path through pullback’s definitional diagram:

In [the] Set [category], the pullback of f: a -> c along g: b -> c is { (a, b) | f a = g b }, which is sometimes undecidable in Haskell [and by extension, Swift].

Hand-waving past Hask and Swift not quite being categories, we reason about them through the category Set.

And Zhu points out that a pullback in Set requires us to equate two functions, f and g in the diagram above, for a subset of inputs and that’s undecidable in programming.

How do we get around this?

Well, setting X to be Y and f to g:

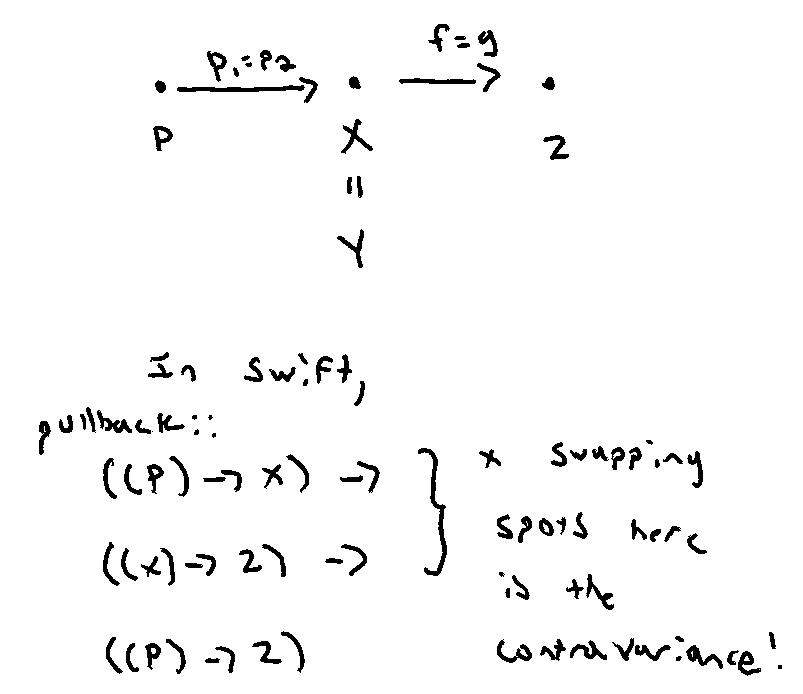
Since pure functions equal themselves, we can sidestep that undecidability by collapsing the diagram. Wickedly clever.

That’s how pullback’s flexibility allows us to consider contramap as a specialization of it.

(un)zurry

16 Oct 2019 (un)zurry moves arguments in and out of Void-accepting closures in the same way (un)curry moves arguments in and out of tuples. Concretely, here’s how they’re defined:

The former is often helpful when staying point-free with functions that are close, but not quite the right shape you need. e.g. mapping unapplied method references:

Eep.

Let’s try to make this work.

We’d like [Int].sorted to have the form [Int] -> [Int], and since SE-0042 got rejected, we have to chisel it down on our own.

First, let’s flip the first two arguments and then address the rogue ().

Getting closer—this is where zurry can zero out the initial Void for us.

zurry(flip([Int].sorted)) // (Array<Int>) -> Array<Int>

Wicked, now we can return to our original example:

[[2, 1], [3, 1], [4, 1]].map(zurry(flip([Int].sorted))) // [[1, 2], [1, 3], [1, 4]].

Dually, unzurry shines when you’re working against a () -> Return interface, that isn’t @autoclosure’d, and you only have a Return in hand. Instead of opening a closure, you can pass along unzurry(yourReturnInstance) and call it a day.

The Point-Free folks link to Eitan Chatav’s post where he introduced the term and shows how function application is a zurried form of function composition (!).

ObservableType.do‌ or .subscribe (Publisher.handleEvents or .sink)?

16 Oct 2019 ObservableType.do‌ or .subscribe?

(The question, rephrased for Combine, involves swapping in Publisher.handleEvents and .sink, respectively.)

do (handleEvents) gives you a hook into a sequence’s events without triggering a subscription, while subscribe (sink) does the same and triggers a subscription—a way to remember this is the former returns an Observable (Publisher) and the latter returns a Disposable (AnyCancellable).

So, when should we use one over the other?

In the past, I’ve always placed effectful work in the do block, even if meant an empty subscribe() call at the end of a chain.

And I’m starting to change my mind here—putting that sole do work in the subscribe block makes the chain more succinct (there are definitely cases where it’s cleaner to use both to sort of group effects, e.g. UI-related versus persistence-related).

I dug up an old bit from Bryan Irace in an iOS Slack we’re a part of that puts it well:

do is for performing a side effect inside of a bigger chain

if all you’re doing is performing the side effect, just do that in your subscribe block